Johann Cervenka Senior Scientist Dipl.-Ing. Dr.techn. Publications

Biography Johann Cervenka was born in Schwarzach, Austria, in 1968. He studied electrical engineering at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1999. He then joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD in 2004. His scientific interests include three-dimensional mesh generation, as well as algorithms and data structures in computational geometry.

For the development of modern electronic devices, often quantum mechanical effects during carrier transport must be accounted for. In the study of solid state physics and electronics, the Schrödinger-Poisson equation is used to describe the behavior of electrons in semiconductor devices. It is defined by a system of two partial differential equations which must be solved self-consistently, meaning that the solution for the wave function and the electric potential must be related in such a way that satisfies both the Schrödinger equation for the wave function and the Poisson equation for the electric potential.

The method iteratively updates the density function and electric potential until a converged solution is obtained. Solving this system is computationally very expensive. In a typical simulation several millions of Schrödinger-type equations need to be solved for the assembly, and a parallelization of the procedure is essential.

As a first attempt, only the most demanding part, the assembly of the Jacobian, was ported to the graphics processing unit (GPU). The problem structure shows a variety of similar independent calculations, which is beneficial for parallelization and transferable to GPUs. For the implementation, we rely on the CUDA platform.

In Fig. 1 the relative speedup of the full calculation of the Jacobian for a one-dimensional nin-structure is shown. The simulation time required for assembling the full Jacobian with one sequential task on the NVIDIA A100 GPU is compared to the parallelized method applying N CUDA tasks on NVIDIA RTX 3070, NVIDIA GTX 1080 Ti, Tesla T4, and A100 GPUs. As a reference, a single thread using one CUDA core on the A100 GPU is about 30 times slower than the same calculation using a single thread on an Intel i7 CPU.

Further steps will be taken in implementing the aggregation of the Schrödinger calculations in parallel, which will further improve the utilization of the GPUs. Additionally, the implementation of the Poisson solver on the GPUs will significantly reduce the amount of memory which must be transferred from/to the GPUs.

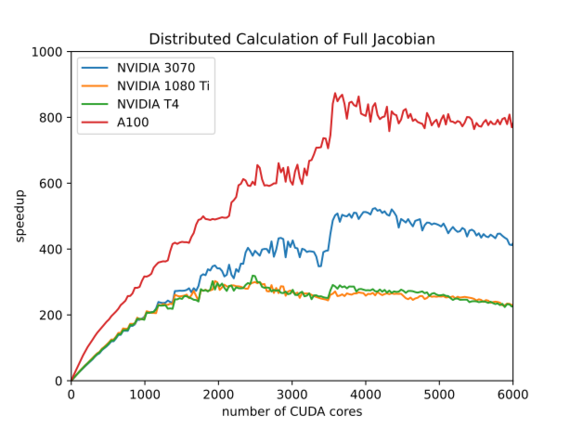
Fig. 1: Achieved speedup for assembling the Jacobian of a Newton step for a nin-structure on GPUs.