Josef Weinbub Associate Prof. Dipl.-Ing. Dr.techn. Publications

Biography Josef Weinbub is an Associate Professor of High Performance Simulation in Micro- and Nanoelectronics, an IEEE Senior Member, and the Vice Chair of the IEEE Nanotechnology Council's Modeling and Simulation Technical Committee. He obtained the doctoral degree in Computational Microelectronics and the venia docendi (habilitation) in the field of Micro- and Nanoelectronics from the TU Wien. He was a visiting researcher at the EPCC, University of Edinburgh and at the Device Modelling Group, University of Glasgow, Scotland, UK as well as at SILVACO Inc., Santa Clara, CA, USA. He founded and now chairs the master’s program Computational Science and Engineering at the TU Wien and is involved with several international scientific conferences in various management and scientific roles. He is an Associate Editor of the Journal of Computational Electronics and a Principal Investigator of various research projects funded by, e.g., the Austrian Science Fund and the Christian Doppler Research Association. Together with his team he investigates cutting-edge research problems in the area of computational micro- and nanoelectronics. Research Interests: Josef’s research interests are focused on developing and utilizing computationally highly demanding simulations in process TCAD and electron quantum transport to study cutting edge challenges in semiconductor fabrication and next generation electron-based quantum devices and systems. Regarding process TCAD, he particularly focuses on parallel algorithm and data structure research with a particular focus on accelerating flux calculations. With respect to electron quantum transport, he focuses on advancing a time-dependent particle Wigner simulation methodology. This is particularly relevant for the field of electron quantum optics, which studies electron-based quantum optics principles (e.g., interference of electron-wave) by being able to control individual electrons. He applies the developed methods by studying dynamic single electron and entangled double electron systems under the influence of electromagnetic fields, and thereby advances the understanding of electromagnetic electron control, coherent electron sources and waveguides, as well as interferometers. Software Development: Particle Wigner Simulator: ViennaWD Research Topics: High Performance Computing Classical and Quantum Transport Process Simulation Running Public Projects: FWF - General Nano-Electromagnetic Quantum Phase Space Model Past Public Projects: CDG - Christian Doppler Laboratory for High Performance TCAD

Tunable barrier quantum dots (QDs) are used in single electron sources which, in turn, are essential building blocks for electron quantum optics, quantum metrology, and quantum information processing. The tunable barriers are realized by a two-gate structure along a nanowire. The operating principle uses a pumping scheme of loading, capture, and ejection stages: Understanding the coherent electron dynamics is vital for optimizing the overall performance. We investigate the dynamics of the captured and ejected electron state by a Wigner simulation study. We consider the probability current and the impact of different timings on the state evolution after ejection. We investigate a one-dimensional nanowire (200 nm) with a QD, which is modeled by two Gaussian potential barriers (see Fig. 1), where the first barrier has a potential energy of V₁=0.5 eV and the second barrier has a time-dependent potential energy of V₂(t), i.e., it is driven by a gate voltage. Up to V₂(t)=V₁, the energy is quantized in the spatial domain bounded by the two Gaussian barriers; the electron state can be obtained, in principle, by the stationary Schrödinger equation as a superposition of the orthonormal set of eigenfunctions ψ_n. We limit our analysis to the first two eigenfunctions of the QD. We use the wavefunction Ψ(x, 0) to determine the density matrix at time t=0 and consequently obtain the initial Wigner function f_w(x, p, 0) which is then evolved by solving the Wigner equation. The coherent dynamics of the superposition state are analyzed by considering the two first moments of the Wigner function, i.e., the probability density n(x) and the probability current J(x). We studied two scenarios: (1) Capture stage: V₂(t) is kept constant and equal to V₁. (2) Ejection stage: V₂(t)=V₁⋅[1-H(t-t₁)], where H(t) is the Heaviside function and particularly considering t₁=10 fs and 400 fs. As the initial condition, we consider the electron to be bounded inside the QD at t=0. Fig. 1 shows the probability density (Wigner and verification with Schrödinger) after a one-half period of oscillation. The electron state oscillates from left to right and vice-versa with a period T≈500 fs. Fig. 2 shows the evolution of the probability density at t=500 fs and t=700 fs for t₁=10 fs, while Fig. 3 shows the same for t₁=400 fs. Different opening times clearly influence the shape of the probability density, potentially leading to separation or superposition.

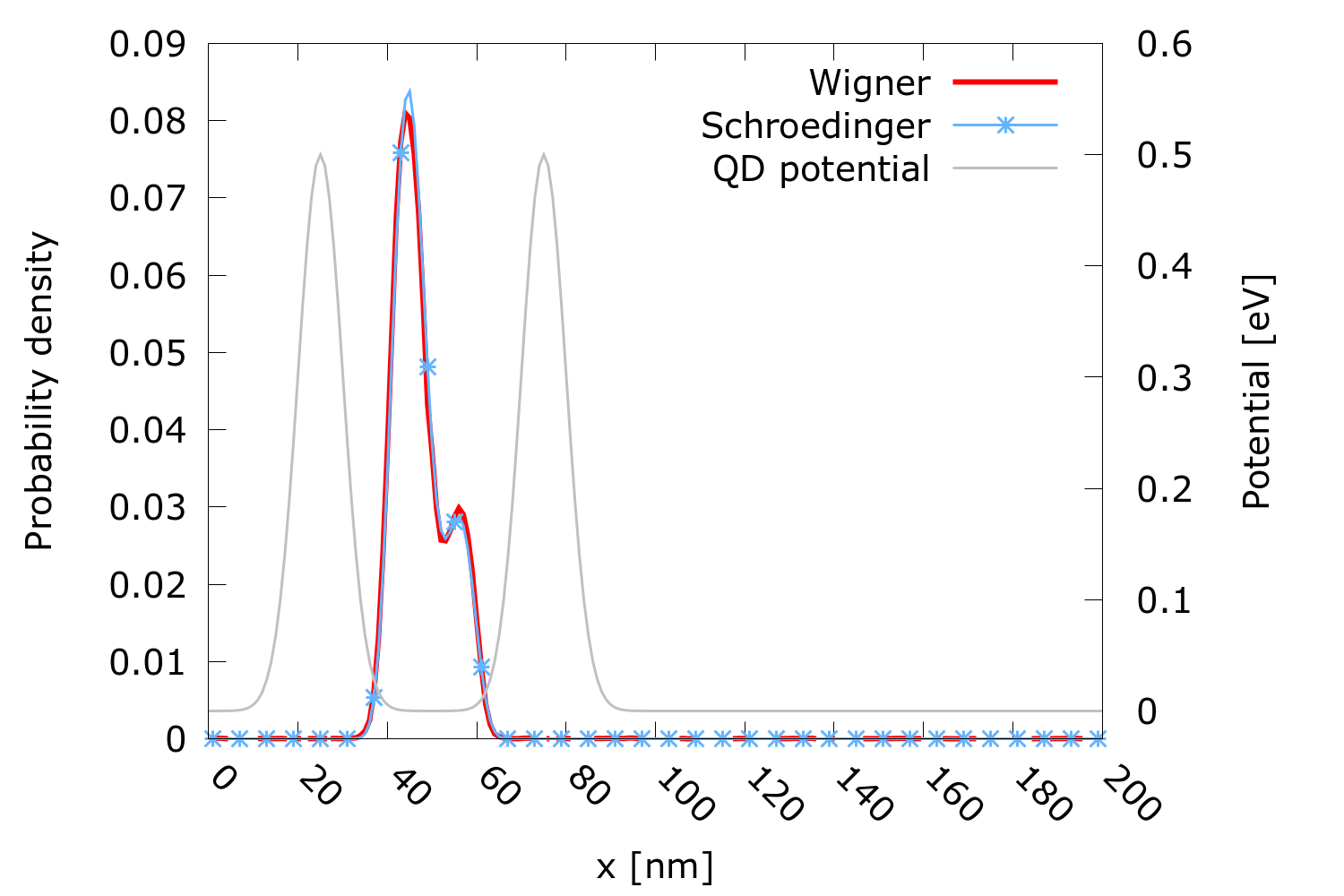
Fig. 1: Probability density of the superposition state at t=250 fs: Comparison between Wigner and Schrödinger. The two peaks of the captured electron state oscillate with T≈500 fs.

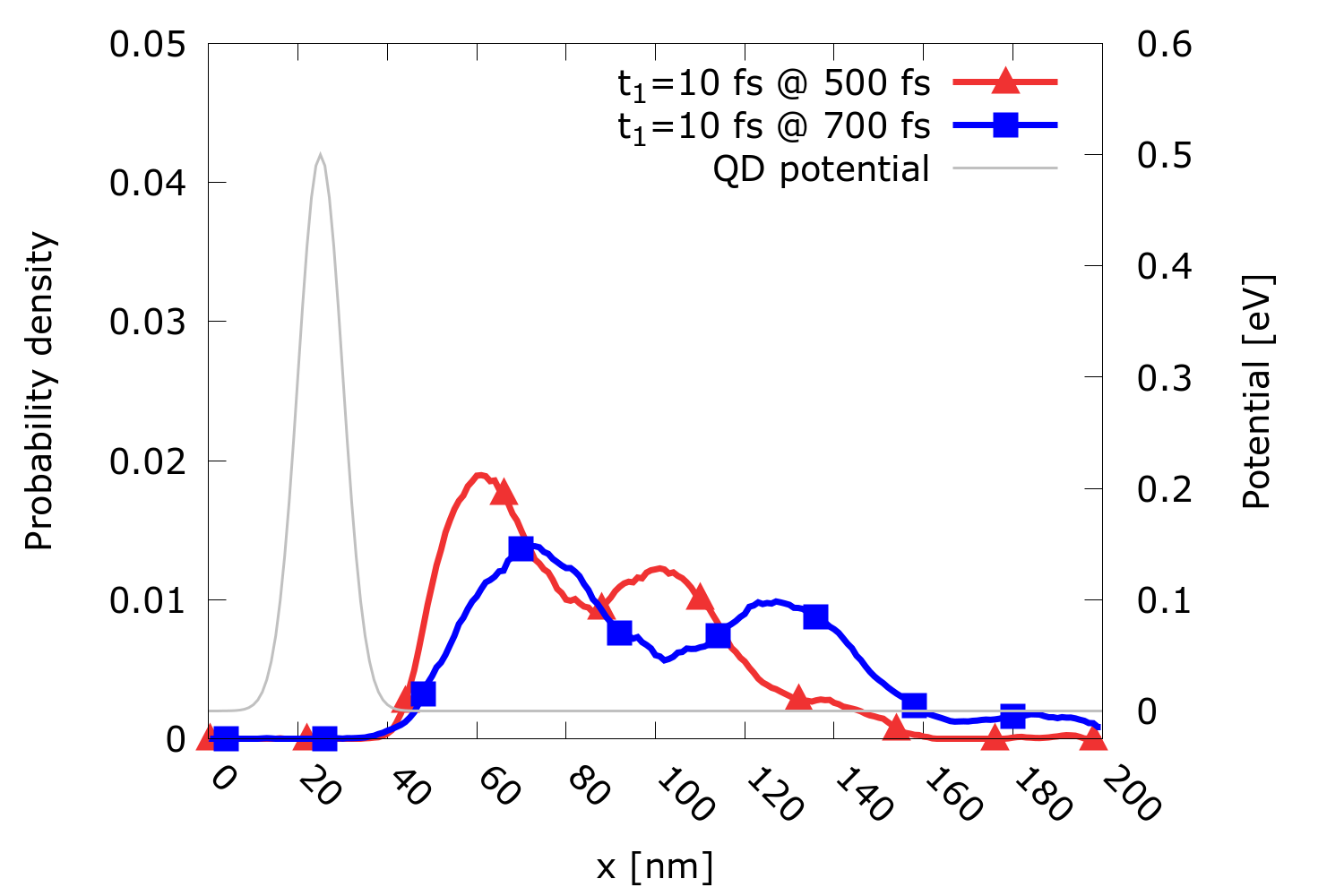
Fig. 2: Evolution along the channel of the electron superposition state ejected at t₁=10 fs: Probability density at t=500 fs and t=700 fs. The state’s peak separation indicates the presence of significantly different velocities (energies) in the state.

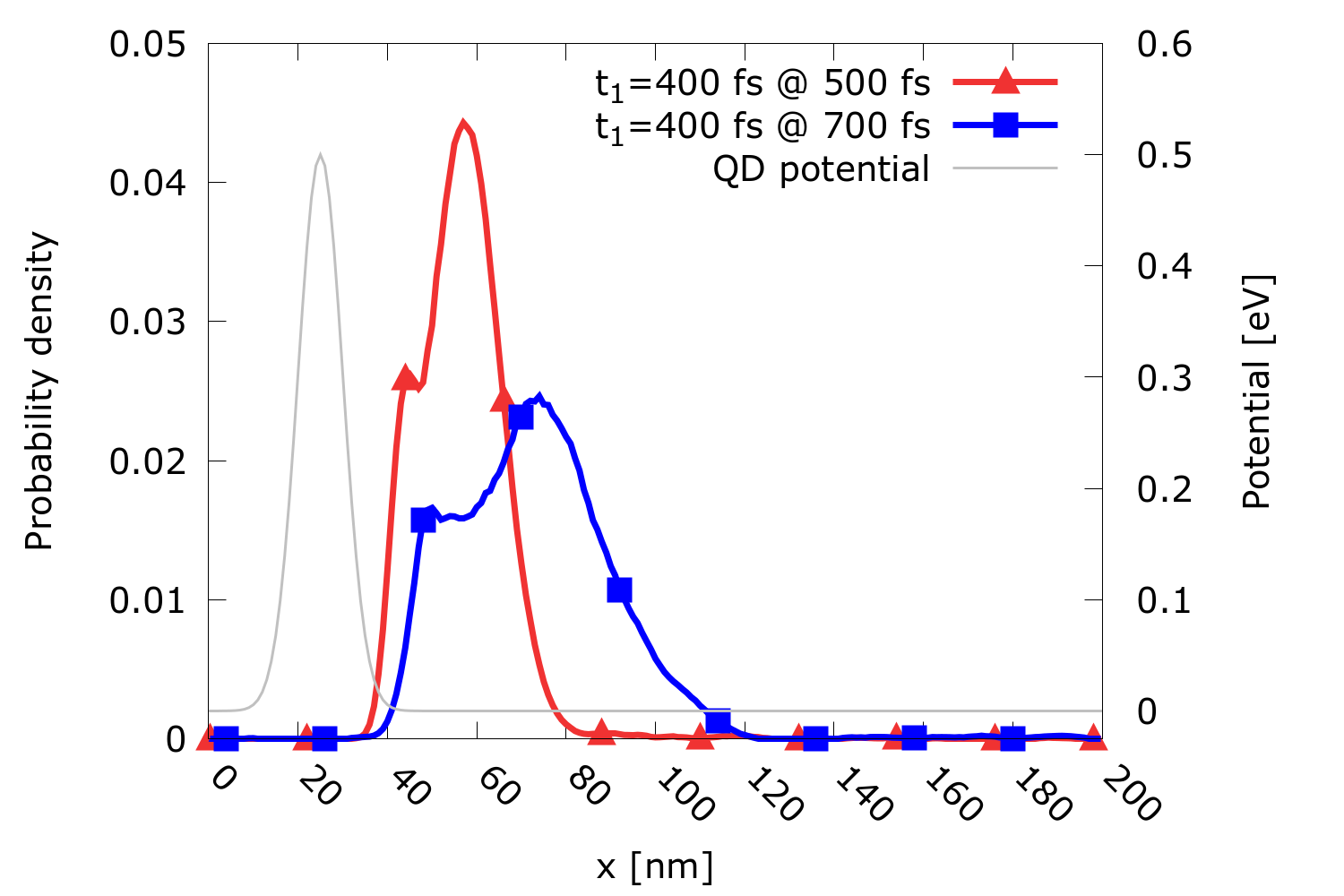
Fig. 3: Evolution along the channel of the electron superposition state ejected at t₁=400 fs: Probability density at t=500 fs and t=700 fs.