 |
|
Biography
Johann Cervenka was born in Schwarzach, Austria, in 1968. He studied electrical engineering at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1999. He then joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD degree in 2004. His scientific interests include three-dimensional mesh generation, as well as algorithms and data structures in computational geometry.
Quantum Evolution over Discrete Phase Space Trajectories
The Wigner formulation of quantum mechanics provides a convenient phase space formulation of quantum theory. Deterministic methods show difficulties in the discretization of the diffusion term in the differential equation because of rapid variations of the Wigner function in the phase-space. The developed approach uses an integral formulation of the Wigner equation of a single fundamental wave packet. In this method the differentiation can be avoided. We consider the evolution of an initial condition described by the superposition (in phase-space) of particular fundamental packages. To calculate the distribution at desired time steps, all "fundamental evolutions" of the Wigner equation have to be summated. The Wigner equation has to be solved for each packet, which only depends on the initial location (in phase-space) of the packet.
Special remarks were placed on memory consumption, parallelization, discretization, and interpolation. Unfortunately, concerning memory consumption, the usual approach to solving each time-step sequential one after the other causes huge memory consumptions for this integral equation. To solve for a particular time-step, each point of phase-space has to know its complete history in time in relation to all other points in phase-space. To overcome this drawback, the solution is found sequentially in phase-space for all time-steps. Here, only the evolving solutions in phase-space have to be stored.
Coming along with this technique, as the particular calculations are independent from each other, this method is well suited for parallelization to reduce calculation times. The different operational points in phase space have been started through several machines by OpenMPI and also in parallel at each of them by OpenMP.
For dense time steps, the solution has shown non-physical behavior due to non-proper discretization of the integral equation. This pitfall was solved by convenient discretization of the integral term.
Additionally, the solution has shown a package speed that is too slow. During evolution in time, the signal shows slow portions in k-space. With the common method by discrete intervals, these parts get cut away. To overcome this issue it was necessary to develop an interpolation between the discrete wave packets.
In Fig. 1 the comparison of an evolving Gaussian wave package during time is shown. The Wigner results are compared with a solution of a Schroedinger solver.
Future investigations on the discretization seem to be necessary. At the beginning, high resolution in phase-space seemed crucial. After applying the proper discretization, it was possible to reduce the resolution. Additionally, it has to be investigated if the size of history in time can be reduced. Both issues will speed up the calculations dramatically.
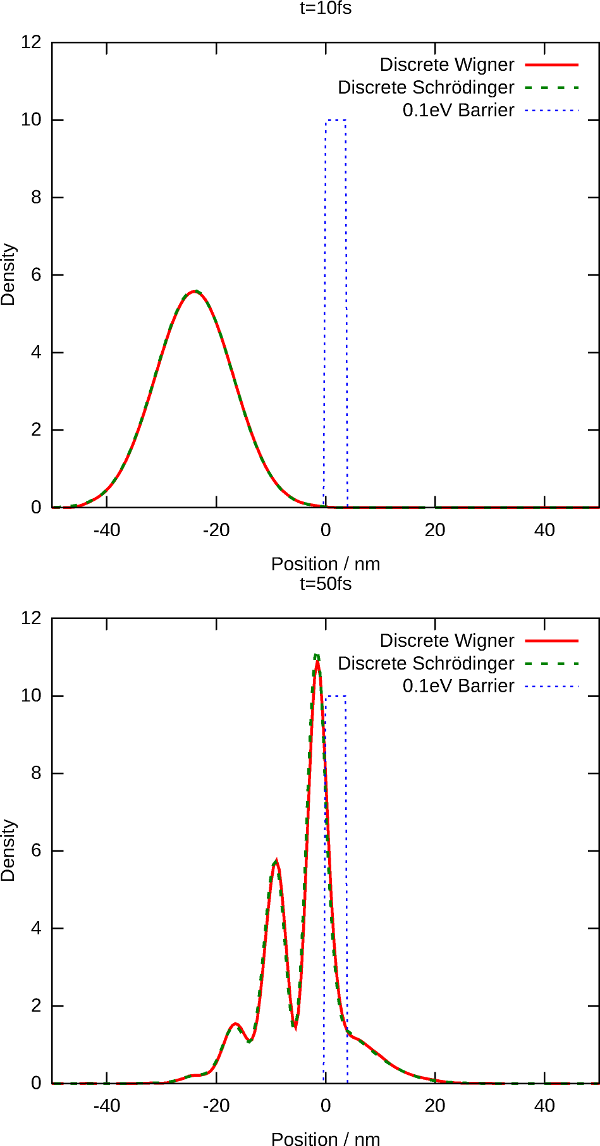
Fig. 1: Density of a wave package moving to the right through a potential barrier after 10fs and 70fs.



