Paul Ellinghaus MSc Publications

The Wigner function provides a formalism to express the quantum mechanical density operator in terms of a quasi-probability distribution, which retains many of the properties of a classical distribution function in the phase space, making it easier to interpret and intuitively understand. The Wigner equation describes the time evolution of the Wigner function making the simulation of quantum transport possible. In addition, classical Boltzmann scattering may be easily incorporated — to form what is known as the Wigner-Boltzmann equation — with a relatively low computational burden, when compared to other approaches, like the non-equilibrium Green's function. The Wigner-Boltzmann equation allows for the time-dependent simulation of realistic electron devices on a mesoscopic scale, treating quantum transport and classical scattering on equal footing. This opens the doorway to investigating fundamental physical phenomena relating to the interplay of quantum and classical effects, like quantum decoherence due to classical scattering.
The research goal is to further develop and improve the quantum Monte Carlo simulator, ViennaWD, that solves the Wigner-Boltzmann equation using the particle-sign method, aiming towards creating a robust simulation tool for nanoelectronic devices. The particle-sign method builds upon the idea of having particles that carry quantum information using a numerical sign. These particles are created with a sign and a momentum offset in accordance to the Wigner potential (Fig. 1), which may be interpreted as a scattering term and yields the probability distributions for creating particles with said quantities. The Wigner potential is at the heart of the particle-sign method. This warrants special consideration being given to the physical assumptions, like the boundary conditions and coherence length, that influence the calculation of the Wigner potential in addition to computationally efficient algorithms to calculate the latter. This has been the focus of research during the past year: a new algorithm was developed that computes Wigner potentials five times faster. In addition, the implications of the (finite) coherence length and windowing functions on the discrete Wigner potential were investigated.

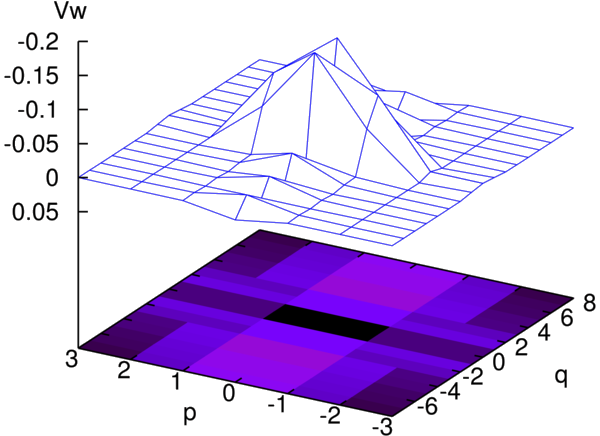
Fig. 1. The 2D Wigner potential, at a fixed position, calculated for a biased Gaussian potential profile yielding the probabilities for creating negative and positive particles with a momentum offset of (p,q).