 |
|
Biography
Mahdi Moradinasab was born in Tehran, Iran, in 1982. He studied electrical engineering at the University of Teheran, where he received the MSc degree in 2009. He joined the Institute for Microelectronics in December 2011. His scientific interests include modeling of optoelectronic and photonic devices.
Dynamics of Quantum Cascade Lasers
Quantum Cascade Lasers (QCLs) are the most prominent and compact coherent light sources in the wavelength range from 3.5μm to 20μm. Remarkable design degrees of freedom make QCLs a unique candidate to serve as a semiconductor source of ultra-short pulses in the Mid-InfraRed (MIR) region. The most common technique for ultrashort pulses is mode locking which is realized either by an internal (passive mode locking) or by an external mechanism (active mode locking). In lasers with a relatively long gain recovery compared to the cavity round-trip time, the instability caused by a Saturable Absorber (SA) can often lead to passive mode locking. Because of ultra-fast tunneling and inter-subband transitions, QCLs, unlike conventional semiconductor lasers, have a shorter gain recovery (in the order of picoseconds) than the cavity round trip time. We investigate the performance optimization and passive mode locking caused by a SA in QCLs. Performance optimization of QCLs has achieved significant progress in recent years. The performance improvement of QCLs can be achieved by optimizing the epitaxial growth, fabrication process, and active region design. The latter is important in order to insure efficient carrier injection in the upper lasing state and carrier extraction out of the lower lasing state. So far, optimization techniques proposed to design QCL structures are based on genetic algorithms. Particle Swarm Optimization (PSO) has been proposed as an alternative to traditional evolutionary algorithms. It attempts to mimic the goal-seeking behavior of biological swarms. Based on the PSO algorithm, we developed a framework for maximizing laser gain with simultaneous desirable instability operation. The effects of the SA and pumping strength on the instability threshold are investigated (Fig. 1). A numerical calculation based on the Maxwell-Bloch equations is performed to analyze the optimized structure. We employ a finite-difference discretization scheme to find the evolution of electric field, polarization, and population inversion in the spatial and time domain.
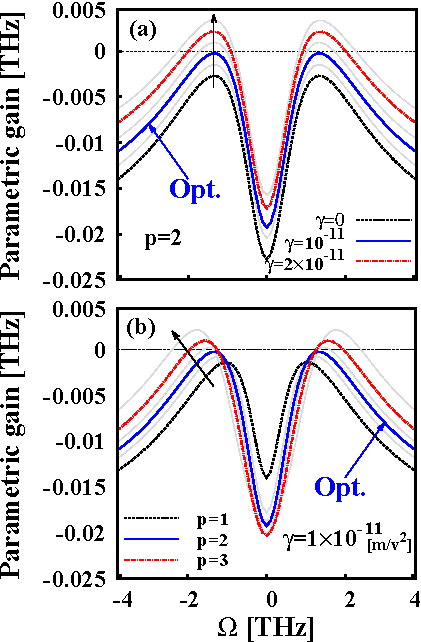
Fig. 1: The parametric gain as a function of the resonance frequency at various (a) SA coefficients and (b) pumping strengths.



