Karl Rupp MSc Dipl.-Ing. Dr.techn. Publications Dissertation

The Boltzmann transport equation is commonly considered to provide the best semiclassical description of carrier transport. However, a numerical solution is very demanding due to the high dimensionality of the phase space. While the Monte Carlo method is the most popular solution approach, the method often results in excessive execution times. As such, the method is usually considered to be too expensive in a productive engineering environment driven by the need for minimizing time-to-market.
The deterministic spherical harmonics expansion method has recently been shown to resolve many of the problems of the Monte Carlo method. In particular, the method allows for execution times in the range of minutes or hours. This is a considerable improvement over the Monte Carlo method, which may take days or weeks to complete if low-probability regimes of the distribution function need to be resolved. For example, so-called hot carrier degradation is caused by a few highly energetic carriers (cf. Fig. 1) for which numerical solutions using the Monte Carlo method are computationally too expensive. To address one of the major drawbacks of the spherical harmonics expansion method, namely, its high mathematical complexity, our free open-source simulator, ViennaSHE, serves as a reference implementation. By making the method easily accessible to other researchers and engineers, we hope to provide valuable contributions to gaining new insights for better device designs.
During the development of ViennaSHE, many challenges needed to be addressed: First, a higher number of code lines as compared to implementations of methods for classical semiconductor models, such as the drift-diffusion model, needed to be maintained and constantly improved. Second, many options and properties needed to be made accessible to the user from the outside, for instance, material parameters. Third, postprocessing functionalities were essential to quickly evaluate the simulation results. Ultimately, the simulator also needed to be as fast as possible, thus requiring us to parallelize the code to efficiently run on multi-core processors as well as on emerging many-core architectures. Therefore, our work on ViennaSHE is an exciting inter-disciplinary endeavor, combining computer science, engineering, mathematics, and physics.

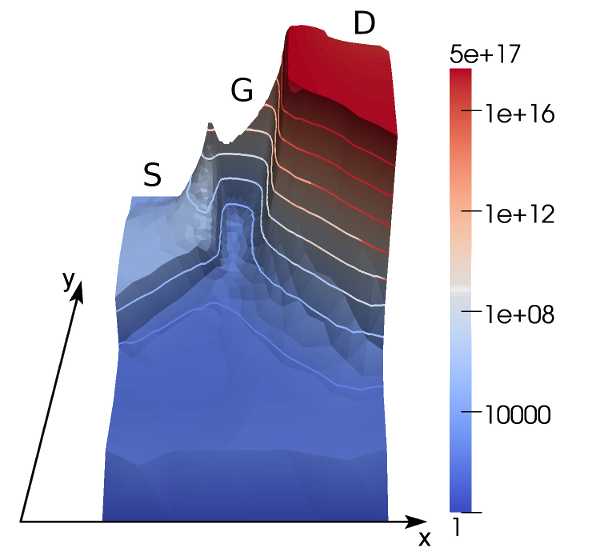
Fig. 1: Density of electrons (per cubicmeter) with a kinetic energy larger than one electronvolt in a metal-oxide-semiconductor field-effect transistor. The higher density of highly energetic carriers in the drain region is clearly visible.