 |
|
Biography
Johann Cervenka was born in Schwarzach, Austria, in 1968. He studied electrical engineering at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1999. He then joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD degree in 2004. His scientific interests include three-dimensional mesh generation, as well as algorithms and data structures in computational geometry.
Ongoing Development on the Deterministic Solution of the Wigner Equation
During the development of modern and future electronic devices, frequently quantum mechanical effects
in carrier transport processes have to be accounted for. In cases such as these, the Wigner formalism provides
a convenient formulation in phase-space. For problems where phase-space quantities vary over several
orders of magnitudes, deterministic solution methods are favored over stochastic approaches.
The problematic discretization of the diffusion term is prevented by the utilization of an integral
formulation of the Wigner equation.
The developed method describes the time-evolution of the solution as a superposition of fundamental wave packages.
Through an examination of the resulting equations, it was possible to dramatically reduce the complexity of
the equation system, and a final reduced set of equations resulted.
Due to the computational costs of the solving mechanism, however, a parallelization of the procedure
is realistically essential in order for results to be obtained. Depending on the problem type, several solution
approaches, which affect the discretization and offer further possibilities for optimization, are feasible.
A dramatical speed up was achieved in systems where the applied potential stays constant in time.
In this case, the partial updates stay constant as well and need only be calculated once
and applied to the distributions of the previous time-step.
However, communication of the actual solution and synchronization among the processes has to be triggered.
Accordingly, areas of low velocities may pose problems. This aspect may not be harmful when using stochastic methods, where
these areas move their discrete position with low probability. For numerical reasons, the deterministic trajectories
may stop evolving, which can be resolved by interpolation of the solution.
Attention has to be paid to the fact that information is lost in this connection, and edges may broaden during this interpolation.
With these approaches, however, the extension of the described method to two dimensions seems feasible.
The development of this is still in progress.
Attention must also be taken on the (at least) second order dependency of spatial and k-space
resolutions on calculation times and memory demands.
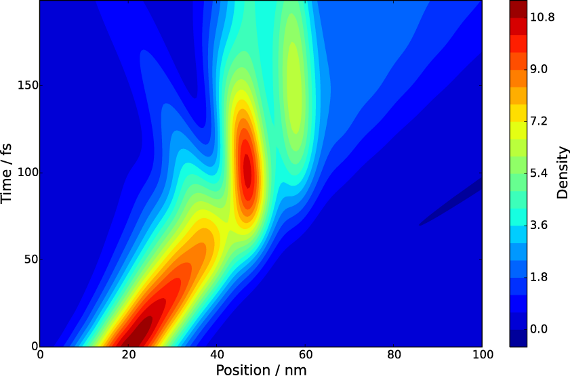
Fig. 1: Propagation of a wave packet through two barriers located at a position of 50 nm and 55 nm



