 |
|
Biography
Robert Kosik was born in Eisenstadt, Austria, in 1969. He studied technical mathematics at the Technische Universität Wien, where he received the degree of Diplomingenieur in 1996. In 1998 he joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD degree in 2004. His scientific interests include partial differential equations for transport modeling and data analysis in reliability.
The Method of Characteristics for Quantum Transport Problems
The simulation of carrier transport processes in modern nano-electronic devices requires a description that uses quantum mechanical models. Two important examples of such models are based on the Wigner equation and the von Neumann Liouville equation. These are linked by a mathematical transformation of the density matrix ρ(x1,x2) to the Wigner function w(r, k). An intermediate step in this transformation requires the introduction of characteristic coordinates. In this coordinate system, the sigma function σ(r, s)=ρ(r+s/2, r-s/2) can be defined. Fourier transformation of σ(r, s) with respect to s gives w(r, k).
We studied properties of the sigma function and its numerical application to quantum transport problems. This is an intermediate representation, which lies between the representations of both the density matrix and the Wigner function. The initial goal of this study was to develop a comparison to Frensley's finite difference Wigner method.
Using coordinates r and s, the stationary von Neumann-Liouville equation takes on its characteristic form, which we call the sigma equation. The sigma equation can be transformed into a two-dimensional integral equation of the Volterra type. Existence and uniqueness of its solution can be proved similarly to the case of ordinary differential equations.
Scattering can be included in a relaxation time approximation using the same models as the finite difference Wigner method. All operators in this equation can be sparsely discretized. The equation can be solved by a shooting method. In this way, a large system matrix does not need to be stored. Furthermore, the method can be easily parallelized. Sparsity of operators can be exploited, which is the main advantage over the finite difference Wigner method.
Discontinuities in the potential operator, resulting from potential steps, can be dealt with by using exact matching conditions. Fig. 1 shows the sigma function corresponding to a partially reflected and transmitted plane wave incident on a step potential.
There is a large body of knowledge on the numerical solution of hyperbolic equations and on Volterra integral equations. These methods need to be adapted and specialized for the solution of the sigma equation. In the future, deeper research into the incorporation of scattering models beyond the relaxation time approximation will be undertaken.
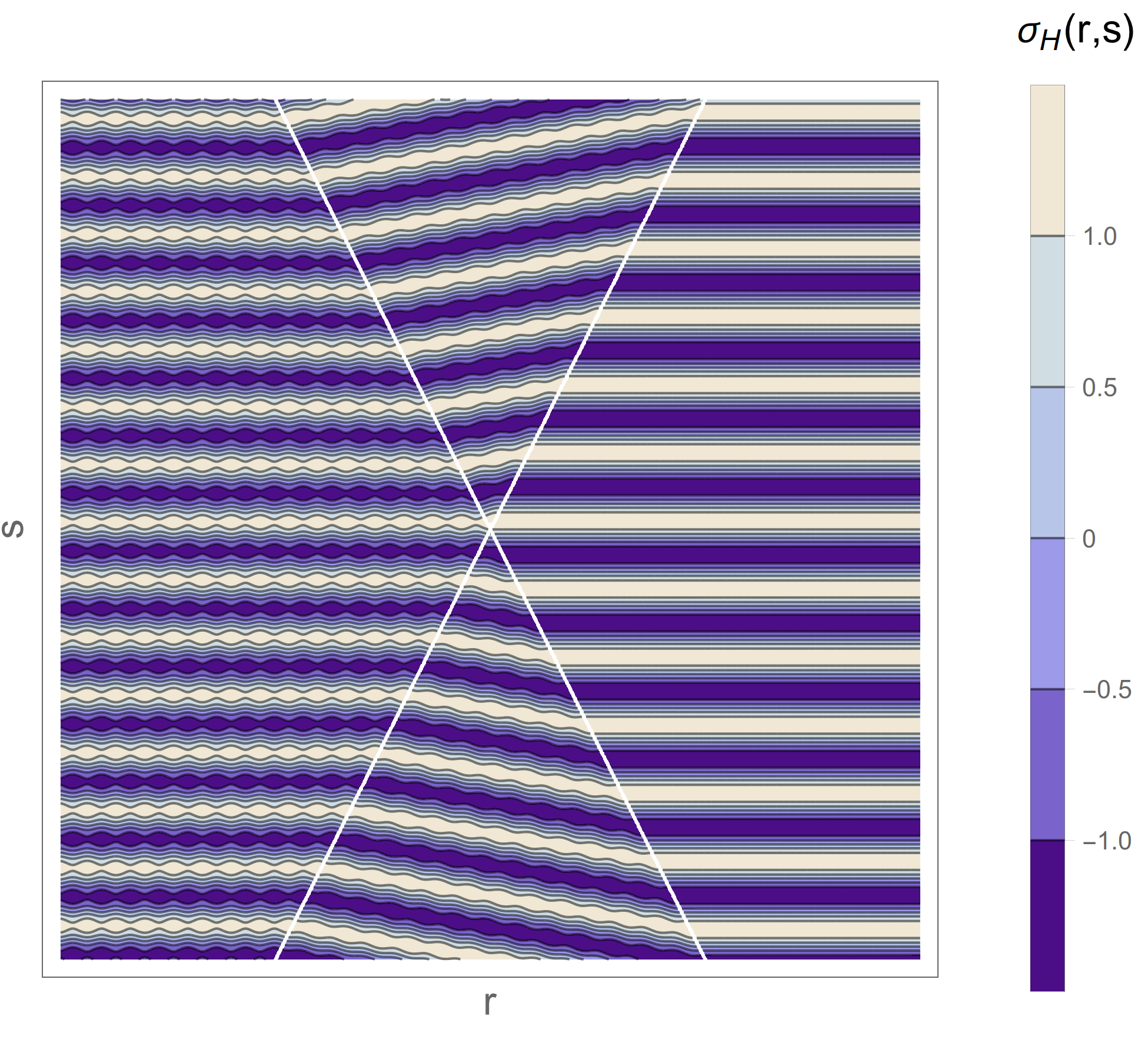
Fig. 1: Sigma function from a plane wave partially reflected and transmitted at a potential step.



