 |
|
Biography
Josef Weinbub holds a bacherlor's degree in electrical engineering, a master's degree in microelectronics, and a doctoral degree in technical sciences from the TU Wien. He was a visiting researcher at EPCC, University of Edinburgh and the Device Modelling Group, University of Glasgow, Scotland, UK. He leads the Christian Doppler Laboratory for High Performance TCAD, where he and his team investigate cutting-edge research problems in the area of high performance process TCAD. In general, however, he conducts research in the field of computational science, with a special focus on software engineering, algorithms, data structures, software frameworks, visualization, and high performance computing.
Evaluation of High Performance Redistancing Methods for Semiconductor Process Simulation
Simulating an expanding front is a fundamental step in many computational science and engineering applications, such as image segmentation, brain connectivity mapping, medical tomography, seismic wave propagation, geological folds, semiconductor process simulation or computational geometry. In general, an expanding front originating from a start position is described by its first time of arrival to the points of a domain. This problem can be described by solving the Eikonal equation. If a constant speed function of 1 is used, the solution represents the minimum Euclidian distance of a point to the interface, henceforth denoted redistancing.
Among the available methods for solving the Eikonal equation are the fast marching method (FMM), the fast iterative method (FIM) and the semi-ordered fast iterative (SOFI) method. In-depth analyses and comparisons have been conducted concerning the performance and the accuracy of these methods to evaluate the suitability for very demanding three-dimensional level-set-based surface evolutions, as used in semiconductor process simulations.
The original FMM is inherently sequential, due to the fact that identifying the smallest solution value is a global process, and previous attempts to parallelize it have been unsatisfactory. Recently, however, a shared-memory parallelization method for the FMM has been developed, which is used for this investigation. The computational domain is partitioned into equal parts (i.e. subdomains) via a static domain decomposition scheme with each thread responsible for a specific subdomain.
The FIM was originally implemented for parallel execution on Cartesian meshes and later extended to triangular surface meshes. Due to its inherently parallel nature, no parallel extension was required, contrary to the FMM and the SOFI methods. The FIM relies on a modification of a label correction scheme coupled with an iterative procedure for the mesh node update. In particular, there is no fixed node update order, and several nodes can be updated simultaneously, enabling parallelism.
Although the FIM provides parallel performance superior to that of other available methods, in most cases, its performance is problem dependent. Complex speed functions tend to increase the solution time significantly. To overcome this shortcoming, the SOFI method has been developed. SOFI is based on both the FIM and so-called two-queue methods. SOFI enforces an ordering to get the iterative behavior closer to front-tracking methods (i.e. fast marching and wavefront tracking methods), in turn offering increased stability when faced with intricate speed functions. Although originally developed as a serial algorithm, the SOFI method has been extended to support shared-memory parallelism.
Fig. 1 illustrates the solution of an exemplary benchmark study. 100 randomly placed source nodes act as boundary conditions for the redistancing. The isosurfaces show the arrival times. Fig. 2 and Fig. 3 show comparisons of the parallel execution times and speedup.

Fig. 1: Solution (isosurfaces) of an oscillatory continuous speed function for 100 randomly placed source nodes. The first time of arrival increases from blue to red.
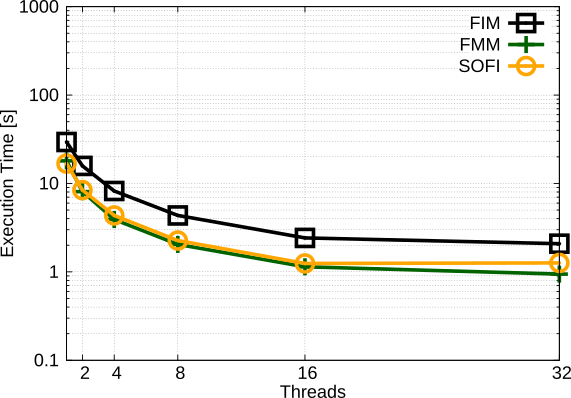
Fig. 2: Comparison of parallel execution times of the FIM, the FMM and the SOFI methods.
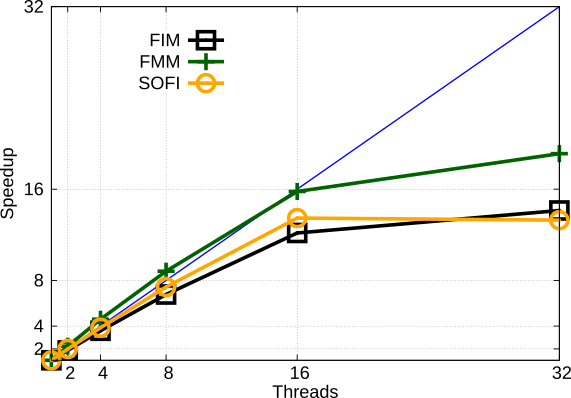
Fig. 3: Comparison of parallel speedup of the FIM, the FMM and the SOFI methods.



