4.2 The First-Order Quantum Corrected Drift Diffusion Model
The density gradient model is first applied to the drift diffusion model (cf. Section 2.3.1), where in
thermal equilibrium the electron concentration is given by
n = NC exp . . | | (4.3) |
Inserting the above relation into Equation (4.2) yields
which gave the model its name ‘density gradient’.
Applying the model to the drift diffusion equations, the quantum corrected drift diffusion equations
now read:
∇⋅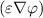 | = ∥q∥(n - p + C), | (4.5)
|
| ∥q∥∂tn -∇Jn | = ∥q∥R, | (4.6)
|
| ∥q∥∂tp + ∇Jp | = -∥q∥R, | (4.7)
|
| Jn | = -∥q∥μn∇x(φ + γn) + ∥q∥Dn∇n, | (4.8)
|
| Jp | = -∥q∥μp∇x(φ + γp) -∥q∥Dp∇p, | (4.9)
|
| γn | = 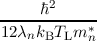  , , | (4.10)
|
| γp | = 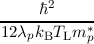  . . | (4.11) |
 .
. .
.
 = -
= -
 ,
,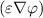
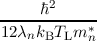
 ,
,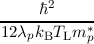
 .
.