4.1 The Density Gradient Model
A method, other than IMLDA, to describe carrier confinement in arbitrary potential wells is called
‘density gradient’ model (DG) [81, 5, 82, 83], which is a first-order quantum-correction model.
Density gradient uses, as its names suggests, the gradient of the carrier densities to describe carrier
confinement by locally modifying the electrostatic potential through a correction potential γ.
Nevertheless, neither the charge carrier wave functions nor the sub band structure can be obtained by
this approach, although it might be possible to assess direct tunneling using DG [83]. The equations
for the correction potential are derived from Wigner’s equation, where it is assumed that any effects
associated with Fermi-Dirac statistics and many-body effects can be safely neglected. Additionally,
the effective mass and parabolic band approximations are used and it is assumed that
the described electron gas has an infinite extent. The correction potential γ(x,t) reads
[82, 83]
γ(x,t) = 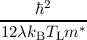  , , | | (4.1) |
where λ is a fitting parameter, which is determined by comparing the carrier density in a MOS
structure to the carrier density obtained by the solution of Equation (2.56). Since the electric field
E = -∇xφ can be undefined at abrupt potential steps, the electrostatic potential φ is replaced, in the
above equation, by φ + γ, yielding
γ(x,t) =   , , | | (4.2) |
which is fine for this first order model, since the error in γ is of second order. This correction potential
has to be calculated separately for each carrier type and added to the electrostatic potential for and
only for the respective charge carrier transport equation.
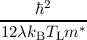
 ,
,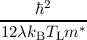
 ,
,
 ,
,