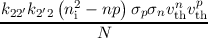Model Evaluation on pMOSFETs using the Direct Current Current Voltage Method

6.4 Model Evaluation on pMOSFETs using the Direct Current Current Voltage Method

In this section a comparison of the SRH model and the four state NMP model using direct current current voltage (DCIV) experiments at various temperatures, conducted using the polyheater technology [153], will be presented. To this end p-type metal-oxide-semiconductor field-effect transistors (pMOSFETs) are studied using the DCIV method before and after bias temperature stress. The ability of the SRH model and the four state NMP model to meaningfully reproduce the acquired DCIV data is compared. It is demonstrated that the SRH model cannot capture the detailed features of the data and that the more detailed four state NMP model is required.

6.4.1 Experimental Setup

For the measurement pMOSFETs with 30 nm thick silicon-dioxide as gate dielectric have been used. All pMOSFETs have been integrated with the polyheater technology presented in [153] in order to be able to locally heat the devices up to 500°C. To monitor the stress induced degradation, DCIV experiments [127, 128] were performed on fresh devices before and after stress using a drain voltage V _d of 0.35 V to forward bias the pn junctions. For each stress temperature a fresh device was stressed for t_s = 10s by applying a gate voltage of -20 V (V _s = -20V and E_ox ≈ 6.7MV∕cm). After 10s of stress the devices were cooled down for t_delay = 200s to room temperature at a gate voltage of -20 V (cf. Figure 6.15) in order to minimize the relaxation during cool down [154] (degradation quenching). With the end of the cool down phase a DCIV curve for the stressed device was recorded.

Figure 6.15:

Time line of a single BTI experiment involving DCIV. From top to bottom the timline of the temperature, gate voltage and drain voltage is shown. In each plot the abscissa has been placed such that it does not interfere with the plot and thus does not correspond to zero on the ordinate. For each stress temperature T_s a fresh device was used. Prior to stress an initial DCIV curve was recorded at room temperature. Afterwards the device was heated by integrated polyheaters almost instantly to the stress temperature T_s, while a gate voltage of -20V was applied. With the end of the bias temperature stress phase the device was cooled down to room temperature (RT). At the end of the cool down phase a DCIV experiment on the degraded device was performed at room temperature (cf. right side of the lower part of the figure).

6.4.2 Comparison of SRH and the four State NMP Model

The standard SRH model for interface traps and the previously introduced four state NMP model for BTI were used to describe the measurement data in order to compare their ability to reflect the (N)BTI stress dependent DCIV data. For the extraction all recombination centers, i.e. stress induced defects, were assumed to be at or near the silicon-oxide interface. During DCIV experiments the bulk current is directly proportional to the number of recombination events [127], simplifying the analysis considerably. It is important to note that any carrier recombination in the bulk, especially at the pn junctions, would cause a constant bulk current during the DCIV experiment. Since we did not observe a shift of the measured DCIV curves along the ordinate within the accuracy of the measurement equipment we can safely assume negligible carrier recombination in the bulk. Geometrical effects could be safely neglected, since large devices with a 30 nm thick gate dielectric and a nominal gate length larger than 100 nm were used. To assess the ability of the SRH model to reflect the DCIV measurement data, the formula originally derived in [155] was used. It reads

R	= ,	(6.51)
U_S^*	= ϕ_s + ln-∕2,	(6.52)
U_TI^*	= ln,	(6.53)

where ni is the intrinsic carrier concentration, EFn and EFp are the quasi Fermi levels for electrons and holes respectively, Ei is the intrinsic energy, σ_p and σ_n are the constant hole and electron capture cross sections, ϕ_s is the surface potential, and β = (kBTL)^-1.

Figure 6.16:

The four state NMP model from [151]. As a first approximation we omitted state 1′ and transitions from/to this state for the DCIV experiments (gray shaded).

In the analysis transitions from/to state 1′ are neglected to obtain a simplified approximation to the full model. Further it was assumed that the DCIV experiment itself does not stress the device any further. This assumption was experimentally justified by comparing DCIV curves for various measurement durations, i.e. different slopes of the gate voltage applied, whereas the measurements yielded the same DCIV curves. With the stated simplification the derivation of a compact analytical version of the carrier recombination rate for the multistate NMP model can be undertaken. By defining effective rates the three remaining defect states have been reduced to only two equvialent states. The effective rates are [156],

k12 =

andk21 =

(6.54)

Employing Maxwell-Boltzmann statistics and applying the assumptions discussed above to the first-order differential for the four state NMP model one obtains

∂_tf = k21(1 - f) - k12f = 0,

(6.55)

for the occupancy of a trap. Using the definition of the recombination rate for holes R^p in steady state and inserting the solution of (6.55), gives an analytical formula in the framework of a multistate NMP model for carrier recombination

R	= -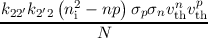	(6.56)
N	= expk22′nσ_nvn th + expk2′2pσ_pvp th
	+ expk2′2niσ_nvn th
	+ expk22′niσ_pvp th,	(6.57)

where vnth and vp th are the electron and hole carrier velocities, σ_n and σ_p are the constant electron and hole capture cross sections. For all simulations the constant capture cross sections σ_n and σ_p were fixed to a value of 2.0 × 10^-16cm² for the SRH and the multistate NMP model.

DCIV curves measured for various stress temperatures, which have been normalized to the peak value for T_stress ≈ 245°C for comparison, are shown in Figure 6.17. The maximum value of the bulk current Ib increases with higher stress temperatures as expected. Also noteworthy is the broadening of the bell-shaped DCIV curve towards negative gate voltages, whereas there is almost no broadening towards positive gate voltages (cf. Figure 6.17 for V _g > -0.5V). This indicates that traps with higher effective activation energies are becoming active trapping centers at higher stress temperatures.

Figure 6.17:

For higher stress temperatures the peak in I_b is larger and the curve is broader towards negative gate voltages (black arrow), whereas the slope for Vg > -0.5V remains nearly constant. Also noteworthy is the reproduceable shoulder towards negative gate voltages for a stress temperature of 315°C.

A fit of the SRH model [136] for the post-stress measurement data is shown in Figure 6.18. It can be seen that the SRH model can reproduce the DCIV curve only for certain stress temperatures (in this case T_stress ≈ 240°C), but not for a wide range of stress temperatures. Especially for stress temperatures above 315°C, when the DCIV bell-shaped curve develops a shoulder towards negative gate voltages, the SRH model cannot reproduce the experimental data as shown in Figure 6.19.

Figure 6.18:

Fits of the standard SRH model to the post-stress DCIV curves for various stress temperatures. Especially for higher stress temperatures, such as 315°C, the standard SRH model cannot reproduce the shape of the measurement data anymore.

Figure 6.19:

Same as in Figure 6.18 but for higher stress temperatures. At very high stress temperatures the post-stress DCIV curve develops a characteristic shoulder. The SRH model cannot predict any of the three DCIV curves, since it cannot reproduce the characteristic shoulder.

Noteworthy is the fact, as seen in Figure 6.19, that the post-stress DCIV curve changes its shape for stress temperatures above 315°C. This is why the SRH model, for which the recombination current exhibits a cosh^-1 shape (cf. (6.51)) for all temperatures [155], cannot reproduce the experimental data anymore. In contrast to the SRH model the four state NMP model can give excellent fits to the data for all stress temperatures as shown in Figure 6.20. This can be attributed to the fact that the reduced four state NMP model additionally considers structural relaxation (cf. Figure 6.16 and Figure 6.22).

Figure 6.20:

In contrast to the fit for the SRH model (cf. Figure 6.18), the NMP model can explain the post-stress DCIV data for all stress temperatures used. Remarkable is the ability of the NMP model to reproduce the DCIV curve for a stress temperature of 315°C with high accuracy.

Figure 6.21:

For high stress temperatures it is possible to reproduce the post-stress DCIV data with good accuracy. Even the characteristic shoulder, best seen for T_stress = 420°C, can be fitted with excellent accuracy.

To understand why structural relaxation can explain the additional shoulder above a stress temperature of 315°C in our data, we reformulated the carrier recombination formulae in the four-state NMP model (6.56) and for the SRH model (6.52) such that both formulas have the same structure. The carrier recombination rate for both models has the following structure

= -

( )
--n2i --np-σ′pσ′nvnthvpth--
τ′(n + n1) + τ′(p + p1)
n p

(6.58)

where τ′_n and τ′_p are the carrier lifetimes for electrons and holes and σ′_n and σ′_p are the capture cross sections for electrons and holes, respectively. These parameters are model-dependent. For the SRH model the capture cross sections have fixed values, where

σ′_n = σ_n = 2.0 × 10^-16cm²,		(6.59)
σ′_p = σ_p = 2.0 × 10^-16cm².		(6.60)

In contrast, the four-state NMP model gives

σ′_n	= σ_n = σ_n,	(6.61)
σ′_p	= σ_p = σ_p.	(6.62)

Furthermore, the carrier lifetimes differ strongly between the SRH model and the multistate NMP model [151]. Thus it can be stated that the effective capture cross sections of the multistate NMP model are device temperature, oxide field and parameter dependent, while those of the SRH model are always constant. By adjusting the energy barriers (ϵ_22′ and ϵ_2′2) describing the structural relaxation (cf. Figure 6.9 and Figure 6.16) it is possible to perfectly fit the DCIV curves measured after high temperature stress (cf Figure 6.21). Figure 6.22 depicts how the shoulder, for stress temperatures above 315°C, can be described using a multistate NMP model. If structural relaxation is neglected (cf state 2 in Figure 6.16) one obtains a standard NMP model [157, 158]. For the standard NMP model the energy barriers (ϵ_22′ and ϵ_2′2) describing the structural relaxation are zero. Thus the effective capture cross sections of the standard NMP model reduce to

σ′_n =

exp(βϵ ′)
------21--
◟k◝2◜2′◞ k◟2◝◜′2◞
1 1

σ_n = exp

σ_n and σ′_p = exp (βϵ ′)
-------12-
k◟2◝2◜′◞◟k◝2′◜2◞
1 1

σ_p = exp

σ_p.

(6.63)

This reduction of the multistate NMP model results in a less pronounced temperature dependence [29] and in the loss of two degrees of freedom for parameter extraction.

Figure 6.22:

When the exchange of charge carriers with the substrate dominates the recombination current exhibits a bell-shaped curve towards negative gate voltages. Whereas when structural relaxation dominates the recombination current exhibits a bell-shaped curve towards positive gate voltages. The weighted sum of these two partial recombination currents gives a bell shaped curve with an additional shoulder [149].

The investigation of the capability of the SRH and NMP model to explain DCIV measurements of pMOS devices after NBTI stress at various stress temperatures shows the importance of structural relaxation for a proper description of recombination currents. A moderate agreement between model and measurement data could be obtained with the conventional SRH model.

[next] [prev] [prev-tail] [front] [up]