Subsections

• 4.1.1 Maxwell's Equations
• 4.1.2 Transport Equations and Mobility
• 4.1.3 Current Density
• 4.1.4 Basic MOS Equations

4.1 Semiconductor Device Equations

The necessary equations which are solved in a numerical device simulator can be obtained from Maxwell's equations and Boltzmann's transport equation.

4.1.1 Maxwell's Equations

In differential and integral form, Maxwell's equations read

$$\ensuremath{{\mathbf{\nabla}}}\times {\mathbf{E}} = -\frac{\partial {\mathbf{B}}} {\partial t}$$	$$\oint_C{{\mathbf{E}}\cdot {\mathbf{dl}}} = -\int_{S}{\frac{\partial {\mathbf{B}}}{\partial t} \cdot {\mathbf{dA}} }$$	Faraday's Law of Induction
$$\ensuremath{{\mathbf{\nabla}}}\cdot {\mathbf{B}} = 0$$	$$\oint_S{{\mathbf{B}} \cdot {\mathbf{dA}}} = 0$$	Gauss's Law of Magnetism
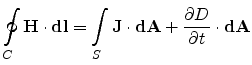$$\ensuremath{{\mathbf{\nabla}}}\times {\mathbf{H}} = {\mathbf{J}} + \frac{\partial {\mathbf{D}}} {\partial t}$$	$$\oint_C{{\mathbf{H}}\cdot {\mathbf{dl}}} = \int_{S}{{\mathbf{J}}\cdot {\mathbf{dA}} + \frac{\partial D}{\partial t} \cdot {\mathbf{dA}} }$$	Ampere's Circuital Law
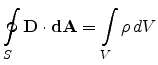$$\ensuremath{{\mathbf{\nabla}}}\cdot {\mathbf{D}} = \rho$$	$$\oint_S{{\mathbf{D}} \cdot {\mathbf{dA}} } = \int_V {\rho dV}$$	Gauss's Law of Electrostatics

Here, ${\mathbf{H}}$ denotes the magnetic field and ${\mathbf{B}}$ the magnetic flux density vector, while ${\mathbf{E}}$ corresponds to the electric field and ${\mathbf{D}}$ to the electric displacement vector. They are related through the equations

$${\mathbf{D}} = \epsilon_0 \epsilon_r {\mathbf{E}}$$ (4.1)

$${\mathbf{B}} = \mu_0 \mu_r {\mathbf{H}} ,$$ (4.2)

where the $\mu_r$ and $\epsilon_r$ denote the relative magnetic permeability and the relative dielectric permittivity of the medium, respectively.

The wavelength associated with an operating frequency of say, $f = 100$ GHz, is given by

$$\lambda = \frac{c}{f} = \frac{c_0} {f\sqrt{\epsilon_r\mu_r}} = 877 \mu m$$ (4.3)

Since $\lambda$ is much greater than the typical device dimensions, which are of the order of $1 \mu m$, a quasi-stationary condition can be assumed for the electric field which can be expressed as a gradient of a scalar potential field,

$${\mathbf{E}} = - \ensuremath{{\mathbf{\nabla}}}{\Phi} .$$ (4.4)

Using (4.1) and (4.4) and Gauss's Law of Electrostatics, we obtain Poisson's equation,

$$\ensuremath{{\mathbf{\nabla}}}{\epsilon_0\epsilon_r} \cdot \ensuremath{{\mathbf{\nabla}}}{\Phi} = - \rho .$$ (4.5)

The space charge density $\rho$ in semiconductors comprises of the mobile charges and the fixed charges. Electrons and holes contribute to the mobile charges while fixed charges are the ionized donors and acceptors,

$$\rho = \mathrm{q} (p - n + C).$$ (4.6)

The $n$ and $p$ denote the electron and hole concentrations and $C$ corresponds to the net doping concentration.

Taking the divergence of Ampere's Circuital Law gives

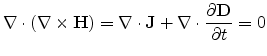$$\ensuremath{{\mathbf{\nabla}}}\cdot (\ensuremath{{\mathbf{\nabla}... ...nsuremath{{\mathbf{\nabla}}}\cdot \frac{\partial {\mathbf{D}}} {\partial t} = 0$$ (4.7)

The current density ${\mathbf{J}}$ in semiconductors is the sum of the electron and hole current densities denoted by ${\mathbf{J_n}}$ and ${\mathbf{J_p}}$.

$$\ensuremath{{\mathbf{\nabla}}}{\mathbf{J}}_n + \ensuremath{{\math... ...t} - \frac{\partial n}{\partial t} + \frac{\partial C}{\partial t} \right) = 0.$$ (4.8)

Considering the fixed charges to be time-invariant $\left(\textstyle\frac{\partial C}{\partial t}=0\right)$, we get

$$\ensuremath{{\mathbf{\nabla}}}{\mathbf{J}}_n - \mathrm{q} \frac{\partial n}{\partial t} = \mathrm{q} R$$ (4.9)

$$\ensuremath{{\mathbf{\nabla}}}{\mathbf{J}}_p + \mathrm{q} \frac{\partial p}{\partial t} = - \mathrm{q} R$$ (4.10)

The quantity $R$ gives the net recombination rate for electrons and holes. A positive value means recombination, a negative value generation of carriers. Equations (4.9) and (4.10) are collectively known as the carrier continuity equations.

4.1.2 Transport Equations and Mobility

Prediction of the I-V characteristics of semiconductor devices requires precise modeling of the mobility. A first principles calculation of mobility begins by describing the state of the electron gas in microscopic terms, followed by set of simplifying assumptions to arrive at macroscopic parameters that can describe the state of the gas collectively. A widely used approach for calculating mobility relies on the Boltzmann transport equation (BTE) which is an integro-differential equation based on both statistical and classical laws of dynamics.

$$\frac{\partial f}{\partial t} + {\mathbf{v}}\cdot \ensuremath{{\m... ...bf{\nabla}}}_{\mathbf{p}} f = \left(\frac{\partial f}{\partial t}\right)_{coll}$$ (4.11)

Figure 4.1: Classification of different scattering mechanisms in Si adapted from [Lundstrom00].

Here $f({\mathbf{r}},{\mathbf{p}},{\mathbf{t}})$ denotes the single particle distribution function, ${\mathbf{v}}$ denotes the group velocity of electrons and ${\mathbf{E}}$ is the applied electric field. The left hand term in (4.11) describes the evolution of the distribution function with time in the six dimensional phase space of coordinates ${\mathbf{r}}$ and ${\mathbf{p}}$ in the presence of externally applied forces. The right hand side term corresponds to the effect of various scattering mechanisms on the distribution function.

Electrons and holes are accelerated by the electric field, but lose momentum as a result of various scattering processes. These scattering mechanisms contributing to the collision term in (4.11) are due to lattice vibrations (phonons), impurity ions, other carriers, surfaces, and other material imperfections. Fig. 4.1 shows a chart describing the various mechanisms of carrier scattering in a semiconductor. The effects of all of these microscopic phenomena are lumped into the macroscopic mobility introduced by the transport equation. However, in its original form, the BTE does not yield a closed form solution for mobility, and only after making certain assumptions, such as the relaxation time approximation, can the solutions be worked out. The resulting mobility can be expressed as

$$\mu = q \langle\tau\rangle \ensuremath{{\underline{m}}}^{-1}$$ (4.12)

where $\langle\tau\rangle$ denotes the average momentum relaxation time and $\ensuremath{{\underline{m}}}$ is the effective mass tensor. The mobility expression in (4.12) is popularly referred to as the Drude model [Drude00]. It is apparent that the value of $\langle\tau\rangle$ directly affects the value of the mobility, and thus characterization of scattering mechanisms helps in estimating the mobility. For Si and Ge, the effective mass tensor is diagonal with equal diagonal components and therefore the mobility can be expressed as a scalar, $\mu$.

In an actual sample of Si, multiple mechanisms can act to scatter the motion of electrons. Based on the assumption of the statistical independence of the scattering mechanisms, the scattering rates may be added using Matthiessen's rule [Nishida87]

$$\frac{1}{\tau} = \frac{1}{\tau_1} + \frac{1}{\tau_2} +\ldots \frac{1}{\tau_n}$$ (4.13)

where $n$ independent scattering mechanisms are involved. The overall mobility is therefore given by

$$\frac{1}{\mu} = \frac{m^\star}{q\tau} = \frac{1}{\mu_1} + \frac{1}{\mu_2} +\ldots \frac{1}{\mu_n}.$$ (4.14)

4.1.3 Current Density

Transport in semiconductors can occur through the application of an electric field or through a gradient of carrier concentrations, temperature or material properties. Taking into consideration the effect of electric field and concentration gradients, an expression for the current density can be obtained from the Boltzmann's transport equation, as shown below.

Making use of the relaxation time approximation (RTA), the collision term on the RHS of (4.11) can be replaced by

$$\left(\frac{\partial f}{\partial t}\right)_{coll} = - \frac{f - f_0}{\tau}$$ (4.15)

where $f_0$ denotes the equilibrium distribution function. Assuming steady state conditions, the one-dimensional BTE can now be written as

$$v_x\frac{\partial f}{\partial x} + \frac{q E}{m} \frac{\partial f}{\partial v_x} = \frac{f_0- f}{\tau}$$ (4.16)

Multiplying (4.16) with $v_x$ and integrating over the three-dimensional velocity space gives

$$\int{ v_x^2\frac{\partial f}{\partial x}d^3v} + \frac{q E}{m} \in... ...partial v_x} d^3v} = \frac{\int{v_x f_0} d^3v - \int{v_x f} d^3v }{\tau}$$ (4.17)

Since the equilibrium function is symmetric, the first integral on the RHS in (4.17) vanishes, and the RHS of (4.17) becomes

$$J_x = - q \int{v_x f d^3 }v$$ (4.18)

and therefore, we have,

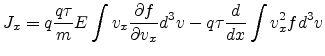$$J_x = q \frac{q\tau}{m} E \int{v_x \frac{\partial f}{\partial v_x}d^3v} - q\tau \frac{d}{dx} \int{v_x^2 f d^3v}$$ (4.19)

Evaluating the integrals in (4.19),

$$\int{dv_y} \int{d v_z} \int{v_x \frac{\partial f}{\partial v_x}dv_x} = \int{dv_y} \int{d v_z} [v_x f]_{-\infty}^{\infty} - \int{f d^3v} = -n$$ (4.20)

$$\int{v_x^2 f d^3v} = n \langle v_x^2 \rangle$$ (4.21)

Introducing the mobility $\mu$ as in (4.12) and the average value $$\langle v_x^2 \rangle$$ as $\frac{k_B T}{m}$, the current density in (4.19) becomes

$${\mathbf{J}}_n = q \mu_n \left [ n {\mathbf{E}} + \frac{kT}{q} \ensuremath{{\mathbf{\nabla}}}n\right].$$ (4.22)

A similar equation is obtained for the hole current density.

$${\mathbf{J}}_p = q \mu_p \left [ p {\mathbf{E}} - \frac{kT}{q} \ensuremath{{\mathbf{\nabla}}}p \right]$$ (4.23)

The Poisson equation (4.5) together with the continuity equations (4.9) and (4.10) and the current density relations (4.22) and (4.23) constitute the fundamental equations for performing drift diffusion based simulations.

4.1.4 Basic MOS Equations

The drain current of an MOS transistor as a function of the gate and drain biases can be computed from the Poisson's equation by making the gradual channel approximation and the charge sheet approximation, as described in [Taur98].

$$\hspace*{-0cm} \ensuremath{I_\mathrm{ds}}= \mu_\ensuremath{{\math... ...V_\mathrm{DS}}}{2\ensuremath{\Phi_\mathrm{B}}}\right)^{3/2} - 1 \right] \right]$$ (4.24)

Here, $\mu_\ensuremath{{\mathrm{eff}}}\prime = \displaystyle \mu_{\mathrm{eff}}C_{\mathrm{ox}}\frac{W}{L}$, with $\mu_{\mathrm{eff}}$ as the carrier mobility and $W$ as the device width and $L$ as the gate length. In the linear regime, where

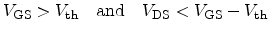$$\ensuremath{V_\mathrm{GS}}> \ensuremath{V_\mathrm{th}}\quad \math... ...suremath{V_\mathrm{DS}}< \ensuremath{V_\mathrm{GS}}- \ensuremath{V_\mathrm{th}}$$ (4.25)

the drain current expression can be simplified to

$$\ensuremath{I_\mathrm{ds}}= \mu_\ensuremath{{\mathrm{eff}}}\prime... ...h{V_\mathrm{GS}}- \ensuremath{V_\mathrm{th}}\right) \ensuremath{V_\mathrm{DS}}.$$ (4.26)

In the saturation regime, where

$$\ensuremath{V_\mathrm{GS}}> \ensuremath{V_\mathrm{th}}\quad \math... ...suremath{V_\mathrm{DS}}> \ensuremath{V_\mathrm{GS}}- \ensuremath{V_\mathrm{th}}$$ (4.27)

the drain current is modeled as

$$\ensuremath{I_\mathrm{ds}}= \mu_\ensuremath{{\mathrm{eff}}}\prime... ...{DS}}- m\ensuremath{V_\mathrm{DS}}^2] (1 + \lambda \ensuremath{V_\mathrm{DS}}),$$ (4.28)

where $\lambda$ denotes the channel length modulation parameter. The quantity $\ensuremath{V_\mathrm{th}}$ denotes the threshold voltage and is obtained as

$$\ensuremath{V_\mathrm{th}}= V_\ensuremath{{\mathrm{fb}}} + (2m-1)2\ensuremath{\Phi_\mathrm{B}}$$ (4.29)

Here $V_\mathrm{fb}$is the flat band voltage

$$\ensuremath{V_\mathrm{fb}}= \ensuremath {\Phi_\mathrm{MS}}- \frac{Q_{\mathrm{ox}}}{C_{\mathrm{ox}}}$$ (4.30)

and $m$ is the body-effect coefficient defined as

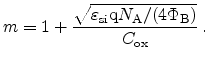$$m = 1 + \frac{\sqrt{\varepsilon_\mathrm{si} \ensuremath {\mathrm{q}}N_\mathrm{A}/(4\ensuremath{\Phi_\mathrm{B}})} } {C_{\mathrm{ox}}} .$$ (4.31)

The potential $\ensuremath{\Phi_\mathrm{B}}$ is evaluated as

$$\ensuremath{\Phi_\mathrm{B}}= \frac{{\mathrm{k_B}}T}{\ensuremath {\mathrm{q}}}\ln\frac{N_\mathrm{A}}{\ensuremath {n_\mathrm{i}}} .$$ (4.32)

In (4.31), $\varepsilon_\mathrm{si}$ is the permittivity of the Si substrate, $N_\mathrm{A}$ the acceptor doping concentration, and $C_{\mathrm{ox}}$ the capacitance per unit area of the oxide. The $n_i$ denotes the intrinsic carrier concentration of Si, $n_i =1.4 \times 10^{10}$   cm$^{-3}$ at 300 K.

From equations (4.26) and (4.28) it is seen that the drain current is directly proportional to the mobility $\mu_{\mathrm{eff}}$. Therefore, employment of strained Si, which enhances the mobility, results in an increase in the drain current, thereby making circuits faster. Moreover, since strain causes a relative shift of the conduction and valence band minima, it can result in a reduced threshold voltage due to a decreased work function difference $\ensuremath {\Phi_\mathrm{MS}}$.