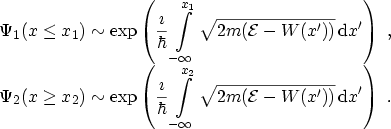B. The WKB Approximation

The WENTZEL-KRAMERS-BRILLOUIN approximation is one of the most frequently applied approximations to solve SCHRÖDINGER's equation [127,130,131]. Starting from the time-independent SCHRÖDINGER equation (2.13), the one-dimensional case reads

$$\left(-\frac{\hbar^2}{2m} \frac{\ensuremath {\mathrm{d}}^2}{\ensuremath {\mathrm{d}}x^2} + W(x) -{\mathcal{E}}\right) \Psi(x) = 0 \ .$$ (B.1)

If the following Ansatz is used for the wave function

$$\Psi(x)=R(x) \exp\left(\imath\frac{S(x)}{\hbar}\right) \ ,$$ (B.2)

the equations

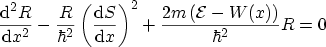$$\frac{\ensuremath {\mathrm{d}}^2R}{\ensuremath {\mathrm{d}}x^2}-\... ...h {\mathrm{d}}x}\right)^2+\frac{2m\left({\mathcal{E}}-W(x)\right)}{\hbar^2}R =0$$ (B.3)

and

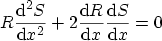$$R\frac{\ensuremath {\mathrm{d}}^2S}{\ensuremath {\mathrm{d}}x^2}+... ...th {\mathrm{d}}x}\frac{\ensuremath {\mathrm{d}}S}{\ensuremath {\mathrm{d}}x} =0$$ (B.4)

for the real and imaginary part of (B.1) can be found. Equation (B.4) can be solved by

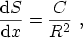$$\frac{\ensuremath {\mathrm{d}}S}{\ensuremath {\mathrm{d}}x}=\frac{C}{R^2} \ ,$$ (B.5)

where $C$ is a constant. With (B.5) equation (B.3) becomes

$$\frac{1}{R}\frac{\ensuremath {\mathrm{d}}^2R}{\ensuremath {\mathr... ...thrm{d}}x}\right)^2 + \frac{2m\left({\mathcal{E}}-W(x)\right)}{\hbar^2} = 0 \ .$$ (B.6)

With the approximation

$$\frac{1}{R}\frac{\ensuremath {\mathrm{d}}^2R}{\ensuremath {\mathr... ...r^2}\left( \frac{\ensuremath {\mathrm{d}}S}{\ensuremath {\mathrm{d}}x}\right)^2$$ (B.7)

we can write

$$S(x) \approx \int \sqrt{2m({\mathcal{E}}- W(x))} \, \ensuremath {\mathrm{d}}x \ ,$$ (B.8)

and the wave function $\Psi(x)$ becomes

$$\Psi(x)=R(x) \exp\left(\frac{\imath}{\hbar}\int{\sqrt{2m\left({\mathcal{E}}-W(x)\right) }\,\ensuremath {\mathrm{d}}x}\right) \ .$$ (B.9)

Now we consider an energy barrier between the classical turning points $x_1$ and $x_2$ with an incoming wave $\Psi_1$ and a transmitted wave $\Psi_2$, and $x_2 > x_1$

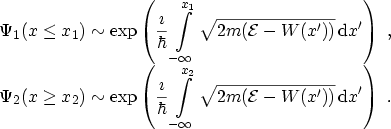$$\renewedcommand{arraystretch}{2.2}\begin{array}{l} \displaystyle ... ...{E}}- W(x^\prime))} \, \ensuremath {\mathrm{d}}x^\prime \right) \ . \end{array}$$ (B.10)

The transmission probability $TC({\mathcal{E}})$ is proportional to $\vert\Psi_2(x_2) / \Psi_1(x_1)\vert^2$:

$$\renewcommand {\arraystretch }{2.8} \begin{array}{rcl} TC &=& \di... ...rime) - {\mathcal{E}})} \, \ensuremath {\mathrm{d}}x^\prime \right) \end{array}$$ (B.11)

This expression can be evaluated for arbitrary barriers as shown in Section 3.5.1. In [130], however, it is shown that the WKB-approximation is only valid for

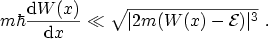$$m\hbar\frac{\ensuremath {\mathrm{d}}W(x)}{\ensuremath {\mathrm{d}}x} \ll \sqrt{\vert 2m(W(x)-{\mathcal{E}})\vert^3} \ .$$ (B.12)

This inequality is fulfilled for points where the variation of the energy barrier is small. The WKB approximation is therefore not valid in the close vicinity of the classical turning points.

A. Gehring: Simulation of Tunneling in Semiconductor Devices