2.4.3.2 WIGNER Equation and the Density-Gradient Model

The WIGNER function is defined as the FOURIER^2.10 transform of the product of wave functions at two points in space [67,68,69]

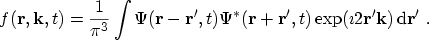$$f(\mathbf{r},\mathbf{k},t) = \frac{1}{\pi^3} \int \Psi(\mathbf{r}... ...th 2 \mathbf{r^\prime}\mathbf{k})\,\ensuremath {\mathrm{d}}\mathbf{r^\prime}\ .$$ (2.18)

Based on the WIGNER function, a transport equation -- the BOLTZMANN-WIGNER equation -- can be derived

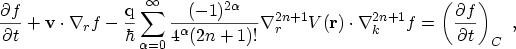$$\frac{\partial f}{\partial t} + {\mathbf{v}} \cdot \ensuremath{{\... ...athbf{\nabla}}}_k^{2n+1} f = \left( \frac{\partial f}{\partial t} \right)_C \ ,$$ (2.19)

where $V$ denotes an external potential. Considering only the $\alpha=0$ term yields the BOLTZMANN transport equation (2.2). If the $\alpha=1$ term is also considered and a parabolic dispersion relation is assumed, the following transport equation, which is frequently referred to as the density-gradient model [70,71,72,73,74,75,76], is found

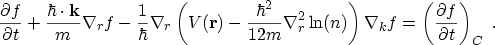$$\frac{\partial f}{\partial t} + \frac{\hbar \cdot {\bf k}}{m} \en... ...ath{{\mathbf{\nabla}}}_k f = \left( \frac{\partial f}{\partial t} \right)_C \ .$$ (2.20)

From this equation the quantum drift-diffusion or quantum hydrodynamic models can be derived by the method of moments. The quantum drift-diffusion model, for example, reads [77]

$$n = \ensuremath {N_\mathrm{c}}\exp\left( \frac{\ensuremath{{\mathca... ...}- \ensuremath {{\mathcal{E}}_\mathrm{c}}- \Lambda}{{\mathrm{k_B}}T} \right)\ ,$$ (2.21)

$$\mathbf{J}_n = -\mu_n {\mathrm{k_B}}T \ensuremath{{\mathbf{\nabla}}}n - \mu_n ... ...\mathrm{c}}- {\mathrm{k_B}}T \ln \ensuremath {N_\mathrm{c}}+ \Lambda \right)\ ,$$ (2.22)

$$\Lambda = -\frac{\gamma \hbar^2}{12\ensuremath{m_\mathrm{eff}}}\left( \en... ...h{m_\mathrm{eff}}}\frac{\ensuremath{{\mathbf{\nabla}}}^2 \sqrt{n}}{\sqrt{n}}\ ,$$ (2.23)

where the correction factors $\gamma$ and $\Lambda$ are used. Thus, the density-gradient model allows a local representation of quantum effects. It is therefore more suitable for the implementation in device simulators than a SCHRÖDINGER-POISSON solver which depends on non-local quantities, for example the thickness of a dielectric layer. The density-gradient method has been used by numerous authors [78,79,80,81,82,83,84,85,86]. However, it was reported that, while the carrier concentration in the inversion layer of a MOSFET can be modeled correctly, the method fails to reproduce tunneling currents as predicted by even more rigorous approaches [77].

A. Gehring: Simulation of Tunneling in Semiconductor Devices