3.4.2 Image Force Correction

When an electron approaches a dielectric layer, it induces a positive charge on the interface which acts like an image charge within the layer. This effect leads to a reduction of the barrier height for both electrons and holes [115,116,117]: The conduction band bends downward and the valence band bends upward, respectively. To account for this effect, the band edge energies (3.47) must be modified

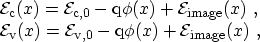$$\begin{array}{l} \ensuremath {{\mathcal{E}}_\mathrm{c}}(x) = ... ... + \ensuremath {{\mathcal{E}}_\mathrm{image}}(x)\ , \end{array}$$ (3.49)

where the image force correction in the dielectric with thickness $\ensuremath{t_\mathrm{diel}}$ is calculated as [118]

$$\ensuremath {{\mathcal{E}}_\mathrm{image}}(x) = - \frac{\ensurema... ...- \vert x\vert} +\frac{2k_1 k_2}{(j+1)\ensuremath{t_\mathrm{diel}}} \right) \ ,$$ (3.50)

where $x=0$ is at the interface to the dielectric. The symbols $k_1$ and $k_2$ are calculated from the dielectric permittivities in the neighboring materials

$$\begin{array}{ll} k_1 = \displaystyle \frac{\ensuremath{\kapp... ...iel}}+ \ensuremath{\kappa_\mathrm{metal}}} = -1 \ . \end{array}$$ (3.51)

Here, $k_2$ accounts for the interface between the insulator and the metal and evaluates to $-1$.

In the semiconductor the band edge energies are also altered

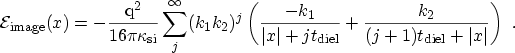$$\ensuremath {{\mathcal{E}}_\mathrm{image}}(x) = - \frac{\ensurema... ...iel}}} + \frac{k_2}{(j+1)\ensuremath{t_\mathrm{diel}}+ \vert x\vert} \right)\ .$$ (3.52)

In practice it is sufficient to evaluate the sums in (3.50) and (3.52) up to $j=11$ [119]. Fig. 3.8 shows the band edge energies in an MOS structure for a dielectric layer with a thickness of 2nm and different dielectric permittivities for an applied bias of 0V (left) and 2V (right). A lower dielectric permittivity leads to a stronger band bending due to the image force and therefore strongly influences the transmission coefficient.

However, there is still some uncertainty if the image force has to be considered for tunneling calculations. While it is used in some works [120,121,122,119], others neglect it or report only minor influence on the results [123,124,125,126,127]. For rigorous investigations, however, its necessary to include it in the simulations. This, however, raises the need for a high spatial resolution along the dielectric. Simple models like the analytical WKB formula or the GUNDLACH formula are not valid for this case, as described in the following sections. It may therefore be justified to account for the image force barrier lowering by correction factors.

Figure 3.8: Effect of the image force in an nMOS device with a dielectric thickness of 2 nm at a gate bias of 0 V (left) and 2 V (right).

A. Gehring: Simulation of Tunneling in Semiconductor Devices