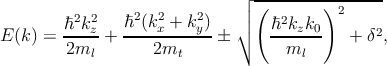3.3 Two-Band k ⋅ p Hamiltonian of [001] Valley at the X-Point
|
|
Parameter | Value |
|
|
Silicon lattice constant | a=0.5431nm |
Spin-orbit term | △SO=1.27meVnm [129] |
Shear deformation potential | D=14eV |
Electron rest mass in silicon | me=9.1093⋅10-31kg |
Transversal effective mass | mt=0.19⋅me |
Longitudinal effective mass | ml=0.91⋅me |
Valley minimum position from X-point | k0=0.15⋅ |
Valley minimum position from Γ-point | k0Γ=0.85⋅ |
M-1 | m
t-1 - m
e-1 |
|
|
| |
Table 3.2: The parameter list for the silicon lattice is shown.
As the lowest two conduction bands Δ1 and Δ2′ (c.f. Figure 3.3) have their
minima just k0 (c.f. Table 3.2) away from the X-point in the Brillouin
zone, a two-band perturbation theory considering only these two bands
developed near the X-point describes the band dispersion and subband
wave functions very well [72]. The two-band k ⋅ p Hamiltonian accurately
describes the bulk structure up to energies of 0.5-0.8eV [72]. However, this
approach is in contrast to [144, 145] where the model has been developed
around the Γ-symmetry point which is far away from the conduction
band minimum and therefore requires a significant increase in considered
bands.
The two-band k ⋅ p Hamiltonian of a [001] valley in the vicinity of the X-point
of the Brillouin zone along the quantization OZ-axis including the shear strain
(εxy) must be of the form [72, 146]
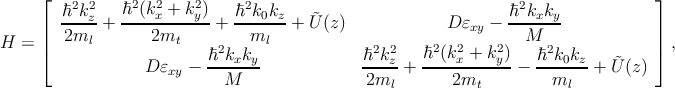 | (3.1) |
where ki with i ∈ x,y,z are the projections of the wave vector on the
coordinate axes, Ũ(z) is the confinement potential, and εxy is the shear strain in
[110] direction. Ũ(z) arises as the UTB silicon film is supposed to be sandwiched
between two oxide layers. The diagonal terms of the (2x2) Hamiltonian
correspond to the Hamiltonian of the individual bands, and the off-diagonal term
signifies the coupling between those two [72].
Hamiltonian including the Spin Degree of Freedom
The corresponding k ⋅ p Hamiltonian including the spin degree of freedom
considering only the relevant [001] oriented valleys written in the vicinity of the
X-point along the OZ-axis in the Brillouin zone can also be derived from
Equation 3.1 by introducing the intrinsic spin-orbit term △SO [71, 129]. △SO
couples the states with opposite spin projections to their respective opposite
valleys. The basis is conveniently chosen as [(X1, ↑) , (X1, ↓) , (X2′, ↑) , (X2′, ↓)],
where ↑ and ↓ indicate the spin projection at the quantization OZ-axis,
X1 and X2′ are the basis functions corresponding to the two valleys.
Thus, the effective (4x4) Hamiltonian with the spin degree of freedom
reads [129, 147]
![[ ]
H = H1 H3 ,
H †3 H2](diss_htm86x.png) | (3.2) |
where H1, H2, and H3 are written as,
![[ 2( 2 2) ]
ℏ2k2z- ℏ---kx-+-ky- (--1)jℏ2k0kz- ˜
Hj=1,2 = 2ml + 2mt + ml + U (z) I](diss_htm87x.png) | (3.3) |
 | (3.4) |
The spin-orbit field (SOF) acts along (kx, -ky) direction. For a zero value of the
confinement potential Ũ(z) the energy dispersion of the lowest conduction bands is
given by [129]
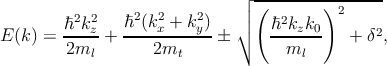 | (3.5) |
where
 | (3.6) |
The ± sign signifies the two bands. This expression generalizes the corresponding
dispersion relation from [71] by including shear strain.
In order to evaluate the effective spin-orbit interaction △SO term one can use
the dispersion relation Equation 3.5. If one evaluates the dispersion for
kx≠0 but ky=kz=0, the gap between the lowest two conduction bands can
be opened by △SO alone in an unstrained sample. The band splitting
along the OX-axis is then equal to 2|△SOkx| and thus linearly related
to kx. This splitting can also be evaluated numerically by the empirical
pseudopotential method, and thereby one can obtain the value for △SO using
the linear fitting technique as described in [129]. △SO is reported to be
1.27meVnm.
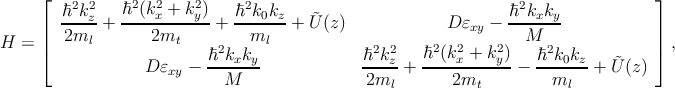
![[ ]
H = H1 H3 ,
H †3 H2](diss_htm86x.png)
![[ 2( 2 2) ]
ℏ2k2z- ℏ---kx-+-ky- (--1)jℏ2k0kz- ˜
Hj=1,2 = 2ml + 2mt + ml + U (z) I](diss_htm87x.png)