



Next: 3.2.2 Energy Relaxation Time
Up: 3.2 Physical Parameters
Previous: 3.2 Physical Parameters
3.2.1 Mobility Model
The mobility model used has proven its usefulness during the last decades
[57]. The temperature dependence of the lattice mobility in
Si is modeled by a power law.
To account for mobility reduction due to ionized impurity scattering, the
formula of Caughey and Thomas [5] is used in
conjunction with temperature dependent coefficients.
CI denotes
the concentration of ionized impurities.
 |
= |
 +
+  |
(3.22) |
 |
= |
 
 |
(3.23) |
Cref |
= |
Cref , 300 . , 300 .  
 |
(3.24) |
 |
= |
 . .  
 |
(3.25) |
Surface scattering is modeled by the following empirical
expression [57]
 |
= |
 |
(3.26) |
 |
= |
 . .  
 |
(3.27) |
| F(y) |
= |
 |
(3.28) |
The pressing forces
Sn and Sp in (3.26) are equal to the magnitude of the
normal field strength at the interface if the carriers are attracted by the
interface, otherwise zero.
For the DD transport model mobility reduction due to a high-field is modeled by
 |
= |
 |
(3.29) |
F |
= |
 grad grad  +
+  . .  . grad . grad  TL . TL . 
  |
(3.30) |
with F representing the driving forces for carrier
representing the driving forces for carrier  .
.
For the HD transport model deviation from the ohmic low-field mobility is
modeled as a function of the carrier temperature, T after
Hänsch [30].
after
Hänsch [30].
 |
= |
 |
(3.31) |
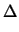 T T |
= |
T - TL - TL |
(3.32) |
 |
= |
 |
(3.33) |
where
 denotes the energy relaxation time.
denotes the energy relaxation time.




Next: 3.2.2 Energy Relaxation Time
Up: 3.2 Physical Parameters
Previous: 3.2 Physical Parameters
Tibor Grasser
1999-05-31
![]() after
Hänsch [30].
after
Hänsch [30].