



Next: 3.2 Mathematical Formulation
Up: 3. Advanced Oxidation Model
Previous: 3. Advanced Oxidation Model
3.1 The Diffuse Interface Concept
The diffuse interface concept avoids a moving interface problem, because there is not a sharp interface between silicon and SiO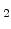 in contrast to the standard models [64,65]. Because of the missing sharp interface there different segments for silicon and SiO
in contrast to the standard models [64,65]. Because of the missing sharp interface there different segments for silicon and SiO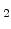 do not exist. In order to determine where is silicon and where is SiO
do not exist. In order to determine where is silicon and where is SiO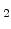 , a parameter named normalized silicon is defined [66]
, a parameter named normalized silicon is defined [66]
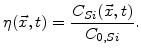 |
(3.1) |
Here
 is the silicon concentration at time t and point
is the silicon concentration at time t and point
 and
and  is the concentration in pure silicon.
is the concentration in pure silicon.  is 1 in pure silicon and 0 in pure silicon dioxide.
is 1 in pure silicon and 0 in pure silicon dioxide.
Instead of a sharp interface there is a so-called reaction layer where the diffusion of oxidants, the chemical reaction, and the volume increase occur simultaneously. This reaction layer has a spatial finite width (see Fig. 3.1), where the values of  lie between 0 and 1 [66]. The
lie between 0 and 1 [66]. The  curve always starts with 0 near silicon and ends at 1 near oxide, as shown in Fig. 3.2. The shape of this curve is given by the calculated
curve always starts with 0 near silicon and ends at 1 near oxide, as shown in Fig. 3.2. The shape of this curve is given by the calculated  distribution in the reaction layer, which depends on the parameters in the model.
distribution in the reaction layer, which depends on the parameters in the model.




Next: 3.2 Mathematical Formulation
Up: 3. Advanced Oxidation Model
Previous: 3. Advanced Oxidation Model
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
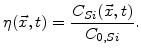
![]() lie between 0 and 1 [66]. The
lie between 0 and 1 [66]. The ![]() curve always starts with 0 near silicon and ends at 1 near oxide, as shown in Fig. 3.2. The shape of this curve is given by the calculated
curve always starts with 0 near silicon and ends at 1 near oxide, as shown in Fig. 3.2. The shape of this curve is given by the calculated ![]() distribution in the reaction layer, which depends on the parameters in the model.
distribution in the reaction layer, which depends on the parameters in the model.