Next: 4.4 Model Overview with
Up: 4. Oxidation of Doped
Previous: 4.2 Five-Stream Dunham Diffusion
If at the Si/SiO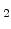 interface there is a dopant concentration
interface there is a dopant concentration  and
and  on the oxide and silicon side, respectively, as illustrated in Fig. 4.1, the segregation coefficient can be written as [83]
on the oxide and silicon side, respectively, as illustrated in Fig. 4.1, the segregation coefficient can be written as [83]
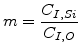 |
(4.23) |
If it is assumed that
 the flux of dopants from the SiO
the flux of dopants from the SiO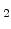 segment to the silicon segment through the interface is [83]
segment to the silicon segment through the interface is [83]
 |
(4.24) |
where  and
and  are the reaction rate coefficients in SiO
are the reaction rate coefficients in SiO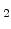 and silicon, respectively.
and silicon, respectively.  is the interface transfer coefficien which has units of velocity.
is the interface transfer coefficien which has units of velocity.
In the steady state the interface flux  and (4.24) can be transformed to the relationship
and (4.24) can be transformed to the relationship
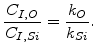 |
(4.25) |




Next: 4.4 Model Overview with
Up: 4. Oxidation of Doped
Previous: 4.2 Five-Stream Dunham Diffusion
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
![]() interface there is a dopant concentration
interface there is a dopant concentration ![]() and
and ![]() on the oxide and silicon side, respectively, as illustrated in Fig. 4.1, the segregation coefficient can be written as [83]
on the oxide and silicon side, respectively, as illustrated in Fig. 4.1, the segregation coefficient can be written as [83]
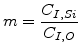
![]() and (4.24) can be transformed to the relationship
and (4.24) can be transformed to the relationship