



Next: 7.2 Stress Calculation Concept
Up: 7. Stress Dependent Oxidation
Previous: 7. Stress Dependent Oxidation
7.1 Oxidation Modeling with Stress
There are two parameters in the oxidation model, which are influenced by stress. The first one is the stress dependent diffusion coefficient [109,110]
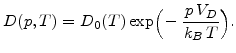 |
(7.1) |
Here  is the low stress diffusion coefficient (3.9),
is the low stress diffusion coefficient (3.9),  is the pressure in the respective material,
is the pressure in the respective material,  is the activation volume,
is the activation volume,  is the Boltzmann's constant, and
is the Boltzmann's constant, and  is the temperature in Kelvin.
is the temperature in Kelvin.
The second parameter is the stress dependent strength of a spatial sink
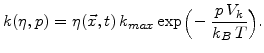 |
(7.2) |
Both parameters are exponentially reduced with pressure, which is only valid for  [111].
[111].
With these two stress dependent parameters the three main equations in the oxidation model, which describe the oxidant diffusion (3.2), the  -dynamics (3.5), and the volume increase (3.8), become
-dynamics (3.5), and the volume increase (3.8), become
The stress is generally described with the formula
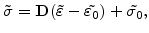 |
(7.6) |
where
 stands for the desired volume increase
stands for the desired volume increase
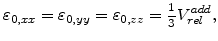 |
(7.7) |
and
 represents the actual volume expansion, because
represents the actual volume expansion, because
 are the partial derivatives of the actual displacements (3.21). On a finite element the mechanical problem
are the partial derivatives of the actual displacements (3.21). On a finite element the mechanical problem
 is loaded by the desired volume increase (
is loaded by the desired volume increase (
 -values) which leads to the internal forces
-values) which leads to the internal forces
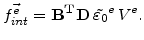 |
(7.8) |
The actual displacements  are obtained after solving the mechanical system (see Fig. 5.5). With these results the actual strains can be calculated
are obtained after solving the mechanical system (see Fig. 5.5). With these results the actual strains can be calculated
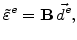 |
(7.9) |
and the stress on an element can be determined with (7.7).
A worth mentioning aspect is the visco-elastic stress computation in the FEDOS simulation procedure. For the actual time step  the visco-elastic stress
the visco-elastic stress
 is the sum of a dilatation and a deviatoric part, because
is the sum of a dilatation and a deviatoric part, because
 as depicted in Section 3.2.5.2. Therefore, also the residual stress
as depicted in Section 3.2.5.2. Therefore, also the residual stress
 for the actual time step
for the actual time step  consists of a dilatation and a deviatoric part so that
consists of a dilatation and a deviatoric part so that
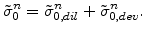 |
(7.10) |
The components of the actual residual stress tensor are build up from the  previous time steps
previous time steps  according to (7.12) for the dilatation and (7.13) for the deviatoric part [112]
according to (7.12) for the dilatation and (7.13) for the deviatoric part [112]
An important characteristic of visco-elastic materials is the stress relaxation of the deviatoric stress components over time with the Maxwellian relaxation time constant  , as given in (7.13). The recursive form for residual stress calculation in the right hand side of (7.12) and (7.13) offers the benefit that the residual stress parts
, as given in (7.13). The recursive form for residual stress calculation in the right hand side of (7.12) and (7.13) offers the benefit that the residual stress parts
 and
and
 at actual time step
at actual time step  can be simply computed by adding the components
can be simply computed by adding the components
 and
and
 from the last step
from the last step  to the already existing residual stress parts
to the already existing residual stress parts
 and
and
 determined at previous step
determined at previous step  .
.
In contrast to stress the pressure needed for (7.1) and (7.2) is a scalar. It is positive, if the com-pressive stress components which have a negative sign, are predominant. So pressure always has an opposite sign compared to stress. The pressure is the average of the stress tensors trace
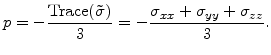 |
(7.13) |




Next: 7.2 Stress Calculation Concept
Up: 7. Stress Dependent Oxidation
Previous: 7. Stress Dependent Oxidation
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
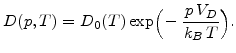
![]() -dynamics (3.5), and the volume increase (3.8), become
-dynamics (3.5), and the volume increase (3.8), become
![]() the visco-elastic stress
the visco-elastic stress
![]() is the sum of a dilatation and a deviatoric part, because
is the sum of a dilatation and a deviatoric part, because
![]() as depicted in Section 3.2.5.2. Therefore, also the residual stress
as depicted in Section 3.2.5.2. Therefore, also the residual stress
![]() for the actual time step
for the actual time step ![]() consists of a dilatation and a deviatoric part so that
consists of a dilatation and a deviatoric part so that