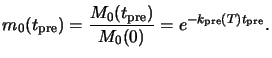7.1.1 Prebake

The purpose of a positive resist prebake is to dry the resist after spin coating by removing solvent from the film. However, when heated to temperatures above 70^oC the PAC concentration M₀ before exposure begins to decompose to a light insensitive product X. The initial reaction mechanism is thereby identical to that of the PAC reaction during UV exposure [78,204] but the dissolution (5.11) is now thermally driven,

 

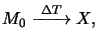$$M_0 @>{\;{\Delta T}\;}>> X,$$ (7.1)

Simple kinetic theory yields^a

 

$$\frac{d M_0(t)}{d t} = -k_{\mathrm{pre}}(T) M_0(t)\qquad\Longrigh... ...qquad M_0(t_{\mathrm{pre}}) = M_0(0) e^{-k_{\mathrm{pre}}(T) t_{\mathrm{pre}}},$$ (7.2)

whereby t_pre denotes the bake time and k_pre(T) is the dissolution rate constant. The dependence of the prebake reaction on the temperature T is modeled by the rate constant k_pre(T). For typical prebake conditions an Arrhenius law can be prescribed, i.e.,

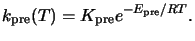$$k_{\mathrm{pre}}(T) = K_{\mathrm{pre}} e^{-E_{\mathrm{pre}}/R T}.$$ (7.3)

Here K_pre is the constant Arrhenius coefficient, E_pre the activation energy, and R the universal gas constant.^b From (7.2) follows that the normalized PAC concentration after the bake takes the form

 

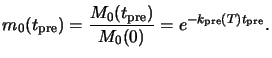$$m_0(t_{\mathrm{pre}}) = \frac{M_0(t_{\mathrm{pre}})}{M_0(0)}=e^{-k_{\mathrm{pre}}(T)t_{\mathrm{pre}}}.$$ (7.4)

The effect of the decomposition (7.2) is a change in the chemical makeup of the resist. Consequently, any parameter depending upon the quantitative composition of the resist also depends upon prebake. The most important ones fall into three categories: (i) optical exposure parameters such as the resist absorption coefficient; (ii) diffusion parameters during post-exposure bake; and (iii) development parameters such as the development rates of unexposed and completely exposed resist. Following [108] we will now briefly describe a measurement technique for the Arrhenius coefficient  K_pre and the activation energy  E_pre.

Dill's classical `ABC'-exposure model does not explicitly take into account the effects of prebake on the resist composition (cf. Section 5.1.2). For that the non-bleachable absorption coefficient B of the resist given in (5.10) has to be modified to include the absorption by the bake products X like

 

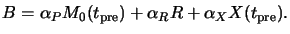$$B = \alpha_PM_0(t_{\mathrm{pre}}) + \alpha_RR + \alpha_XX(t_{\mathrm{pre}}).$$ (7.5)

Here $\alpha_{X}^{}$ is the molar absorption coefficient of the decomposition product X. The stoichiometry of (7.1) gives X(t_pre) = M₀(t_pre) - M₀(0) so that

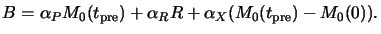$$B = \alpha_PM_0(t_{\mathrm{pre}}) + \alpha_RR + \alpha_X(M_0(t_{\mathrm{pre}})-M_0(0)).$$ (7.6)

Considering now the two extreme cases of no bake (NB) at all and full bake (FB) corresponding to the situation when all PAC is decomposed, we get (cf. (5.10) and (7.5))

 

$$\begin{alignedat}{2}{\text{no bake:}} \qquad& A_{\mathrm{NB}}=(\a... ...rm{FB}}=0, &\qquad B_{\mathrm{FB}} &= -\alpha_XM_0(0)+\alpha_RR.\end{alignedat}$$

These two special cases show how the Dill A and B parameters vary with the normalized PAC decomposition  m₀(t_pre) of (7.4):

 

$$A=A_{\mathrm{NB}}m_0(t_{\mathrm{pre}}) {}\qquad{\text{and}}\qquad{}B=B_{\mathrm{FB}}+(B_{\mathrm{NB}}-B_{\mathrm{FB}}) m_0(t_{\mathrm{pre}}).$$ (7.7)

The bleachable absorption coefficient A decreases proportional to the PAC concentration m₀(t_pre) after the prebake, whereas the non-bleachable coefficient B only slightly depends on m₀(t_pre). It decreases if $\alpha_{P}^{}$ > $\alpha_{X}^{}$ and decreases otherwise (cf. (7.7) and (7.8)). In Figure 7.1 the dependence of the resist absorption parameter A on prebake time t_pre for a specific resist is shown. The plots exhibits a time lag before the decomposition occurs. The reason is a warm-up time of the wafer. In the given example approximately 12 minutes are required to bring the wafer on the elevated temperature. From these data the Arrhenius coefficient  K_pre $\cong$ 1.65 10²⁰ 1/minutes and the activation energy  E_pre $\cong$ 163.59 kJ/mol can be extracted.

  

Figure 7.1: Dependence of the Dill absorption parameter A on prebake time t_pre for the KODAK 820 resist at a wavelength of 365 nm (after [205]).

Footnotes

... yields^a

Here we assume that the PAC concentration M₀ is homogeneous.

... constant.^b

The universal gas constant equals R = kN_A with the Boltzmann constant k $\cong$ 1.38 10^-23 J/K and the Avogadro number N_A $\cong$ 6.02 10²³ 1/mol. R has a value of R $\cong$ 8.31 J/K mol.