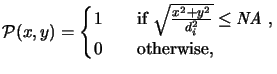Next: 4.1.3 Fourier Analysis of
Up: 4.1 Principles of Fourier
Previous: 4.1.1 Scalar Diffraction Theory
A thin lens acts as a phase transformation, if a ray entering at coordinates
(x, y) on one face emerges at approximately the same coordinates on the
opposite face, i.e., if there is negligible translation of the ray within
the lens. The phase-change of the ray is given by
with  as the refractive index of the material of the lens,
as the refractive index of the material of the lens,
 as the thickness of the lens on the optical axis, and
as the thickness of the lens on the optical axis, and
 (x, y) as the thickness function.
The calculation of the thickness function is shown in
Figure 4.2,
(x, y) as the thickness function.
The calculation of the thickness function is shown in
Figure 4.2,
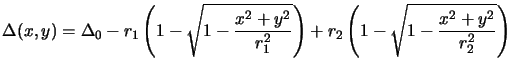 |
(4.14) |
and writes with the paraxial approximation [111, p. 80] to
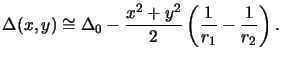 |
(4.15) |
The paraxial approximation assumes that the lateral extent (x, y) of the
lens is small as compared to the curvature radii r1 and r2, i.e.,
(x2 + y2)max  r1, r2.
r1, r2.
Figure 4.2:
Thickness function of a thin lens.
|
|
The lens transformation is simply given by
 |
(4.16) |
where l (x, y) and
 (x, y) are the phase transfer function and
pupil function of the lens, respectively,
and
Ul1(x, y) and
Ul2(x, y) are the
fields entering and emerging the lens.
Suppressing the irrelevant constant phase shift
k0
(x, y) are the phase transfer function and
pupil function of the lens, respectively,
and
Ul1(x, y) and
Ul2(x, y) are the
fields entering and emerging the lens.
Suppressing the irrelevant constant phase shift
k0 the
phase transfer function follows from (4.16),
the
phase transfer function follows from (4.16),
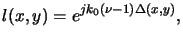 |
(4.17) |
and can be simplified with the paraxial approximation (4.18) like
 |
(4.18) |
Here, f denotes the focal length that combines all physical properties
of the lens, i.e., the refractive index  and the two curvature
radii r1 and r2.
and the two curvature
radii r1 and r2.
The pupil function
 (x, y) describes the pass region of the lens. For
an ideal diffraction limited circular lens centered on the optical axis
(x, y) describes the pass region of the lens. For
an ideal diffraction limited circular lens centered on the optical axis
 (x, y) is
given by
(x, y) is
given by
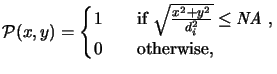 |
(4.19) |
where
NA is the numerical aperture and di the distance between
the image position and the lens plane. The numerical aperture describes
the width of the collection cone
at the image side and is defined as the sine of the half-collection angle
 , i.e.,
, i.e.,
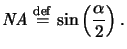 |
(4.20) |
A schematic is shown in Figure 4.3.
Note that we have defined the numerical aperture at the image side. An analog
definition at the object side is possible, but in this case the magnification
of the lens has to be considered.
Figure 4.3:
The numerical aperture
NA of a
lens is the sine of the half-angle  /2 of the collection cone at the
image side. An analog definition exists for the object side.
/2 of the collection cone at the
image side. An analog definition exists for the object side.
|
|




Next: 4.1.3 Fourier Analysis of
Up: 4.1 Principles of Fourier
Previous: 4.1.1 Scalar Diffraction Theory
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17


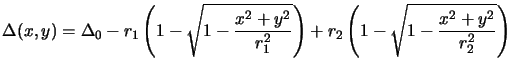
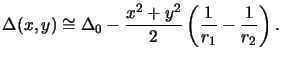

![]() (x, y) describes the pass region of the lens. For
an ideal diffraction limited circular lens centered on the optical axis
(x, y) describes the pass region of the lens. For
an ideal diffraction limited circular lens centered on the optical axis
![]() (x, y) is
given by
(x, y) is
given by