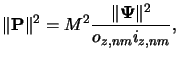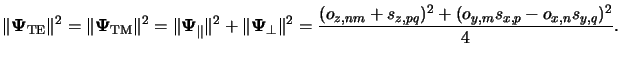Next: 4.2 Lens Aberrations and
Up: 4.1 Principles of Fourier
Previous: 4.1.4 Köhler Illumination of
4.1.5 Vector-Valued Extension
The preceding derivation of the scalar theory of Fourier optics
neglects the vector nature of light. For high numerical aperture systems,
e.g., for
NA = 0.5 and above, the approximations and
simplifications made throughout fail and
the oblique propagation of the waves becomes important.
The most obvious vector diffraction effects arise from polarization
in the illumination producing orientation-dependent asymmetries in the
printed patterns. For example, in the case of phase-shifting masks
or off-axis illumination the aerial image strongly depends on
whether polarization parallel or perpendicular to the lines and spaces is
used. In this section we follow the imaging part of Yeung's key
work [114] and summarize the fundamental results therefrom using
our notation.
The scalar amplitude U(x, y) used so far
has to be replaced by vector functions
E(x, y) and
H(x, y) representing the electric and magnetic field,
respectively. Assuming again a periodic mask, the two field vectors
can be expanded into a plane wave superposition corresponding
to the Fourier series of (4.51):
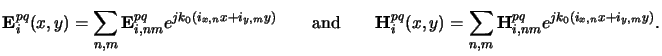 |
(4.51) |
The lateral components ix, n and iy, m of the wavevectors
inm belonging to the image space
follow from (4.47) to
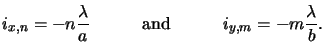 |
(4.52) |
Note that the magnification M is eliminated because
inm is
defined in the image space. The Fourier coefficients
Ei, nmpq
and
Hi, nmpq in the above plane wave expansion are--similar
to (4.52)--given by
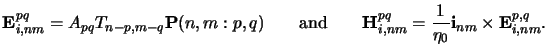 |
(4.53) |
The right equation ensures that the electric, magnetic, and orientation vector
form a right-handed orthogonal triad.
The left equation is equivalent to the scalar
formula (4.52).
Instead of the scalar pupil function P(n, m) we have now
a vector-valued pupil function
P(n, m : p, q)
that also depends on the source point position (p, q)
beside the diffraction order (n, m).
Following [114] we write
P(n, m : p, q) as
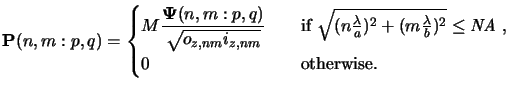 |
(4.54) |
Here,
 (n, m : p, q) denotes the polarization vector.
For further calculations it is convenient to decompose the polarization vector
(n, m : p, q) denotes the polarization vector.
For further calculations it is convenient to decompose the polarization vector
 (n, m : p, q) into a transversal-electric (TE) and a
transversal-magnetic (TM) mode.
In case of TE-illumination the y-component of the electric field vanishes
in the source space, for TM-illumination the magnetic field in the image space
is transverse to the y-axis. The overall polarization state is composed like
(n, m : p, q) into a transversal-electric (TE) and a
transversal-magnetic (TM) mode.
In case of TE-illumination the y-component of the electric field vanishes
in the source space, for TM-illumination the magnetic field in the image space
is transverse to the y-axis. The overall polarization state is composed like
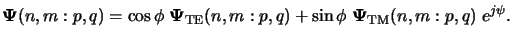 |
(4.55) |
The two vectors
 TE(n, m : p, q) and
TE(n, m : p, q) and
 TM(n, m : p, q) are orthogonal and the two angles
TM(n, m : p, q) are orthogonal and the two angles  and
and
 determine the actual polarization state. The illumination is said to
be linearly polarized in
(cos
determine the actual polarization state. The illumination is said to
be linearly polarized in
(cos , sin
, sin )-direction if
)-direction if  = 0,
circularly polarized for
= 0,
circularly polarized for
 =
=  /4 and
/4 and
 =
=  /2, and
elliptically polarized otherwise. In case of unpolarized light the images for
TE- and TM-modes have to be calculated separately with
/2, and
elliptically polarized otherwise. In case of unpolarized light the images for
TE- and TM-modes have to be calculated separately with
 =
=  /4 and
incoherently superposed afterwards.
/4 and
incoherently superposed afterwards.
Expressions for the two fundamental modes are found by tracing the
ray paths through the optical system as illustrated in
Figure 4.6.
For the sake of definiteness we first summarize the discretization of the
wavevectors occurring in the three relevant spaces:
As can be seen, the three vectors
spq,
onm, and
inm lie in a common
plane usually called meridional plane. Due to singularities the
following two different cases have to be studied separately.
The derivation of the provided formulae can be found in [114].
- Vertical incident ray or
(n, m) = (0, 0).
The TE- and TM-polarization vectors are given by
- Oblique incident rays or
(n, m)
 (0, 0).
Here, the TE- and TM-polarization vectors are further decomposed into a parallel
and perpendicular vector to the meridional plane, i.e.,
The two amplitudes
(0, 0).
Here, the TE- and TM-polarization vectors are further decomposed into a parallel
and perpendicular vector to the meridional plane, i.e.,
The two amplitudes
 (n, m : p, q) and
(n, m : p, q) and
 (n, m : p, q) are
given by
and the two unit vectors
(n, m : p, q) are
given by
and the two unit vectors
 || (n, m) and
|| (n, m) and

 (n, m) equal to
(n, m) equal to
Figure 4.6:
Ray path
through a schematic projection system. The three wavevectors
spq,
onm, and
inm lie in a
common plane, the so-called meridional plane of the optical system.
|
|
The norm
|P| of the vector-valued pupil functionm
will be of interest for
the energy normalization in case of more than one illuminating
point source (cf. Section 4.3.1).
It follows from (4.58) to
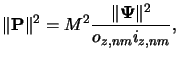 |
(4.57) |
whereby due to the orthogonality of the fundamental TE- and TM-modes
the norm
| | of the polarization vector obeys
| of the polarization vector obeys
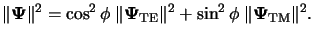 |
(4.58) |
It can be further shown that the following relation holds:
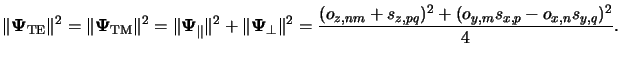 |
(4.59) |
Finally, the image intensity
Iipq(x, y) due to one source point excitation
(p, q) equals to the vertical component of the Poynting vector
Sipq = Eipq x Hipq, i.e.,
![$\displaystyle I_i^{pq}(x,y) = \Big[\mathbf{E}_i^{pq}(x,y)\times\mathbf{H}_i^{pq}(x,y)\Big]_z.$](img540.gif) |
(4.60) |
Footnotes
- ... functionm
- For
the sake of a compact notation we suppress the dependence on the indices
(n, m) and (p, q) for the moment.




Next: 4.2 Lens Aberrations and
Up: 4.1 Principles of Fourier
Previous: 4.1.4 Köhler Illumination of
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
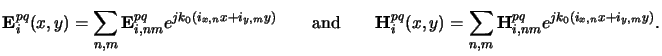
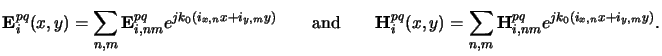
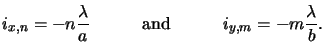
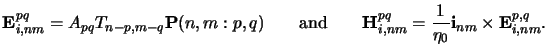
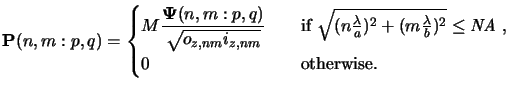


![$\displaystyle \begin{aligned}\Psi_\parallel(n,m:p,q) &= \frac{1}{2\sqrt{i_{x,n}...
...}s_{x,p}s_{y,q}-i_{y,m}(1-s_{y,q}^2)-o_{z,nm}i_{y,m}s_{z,pq}\Big],\end{aligned}$](img529.gif)