


Quantum cascade lasers (QCLs) are the most prominent and compact coherent light sources in the wavelength range from 3.5 to 20 µ m. Remarkable design degrees of freedom make QCLs a unique candidate to serve as a semiconductor source of ultrashort pulses in the mid-infrared (MIR) and terahertz (THz) regions [123, 185, 186]. Ultrashort pulses which are generated in QCL media have been employed for various applications, such as non-linear frequency conversion [187, 188], high-speed free space communication [189], and trace gas detection [190].
A common technique for generation of ultrashort pulses is mode locking which is realized either by an internal mechanism (passive mode locking) or an external one (active mode locking) [191]. Active modelocking does not lead to ultrashort pulses, because the frequency of modulation cannot be raised arbitrarily while a passive saturable absorber is much more effective in ultrashort pulse generation [128]. In lasers with a relatively long gain recovery time compared to the cavity round-trip time, the instability caused by a saturable absorber (SA) can often lead to passive mode locking [128]. Because of ultra-fast tunneling and inter-subband transitions, QCLs, unlike conventional semiconductor lasers, have a gain recovery (in the order of picoseconds) faster than the cavity round trip time. Therefore, SA dominated self-mode locking seems impossible in typical QCLs. However, as reported in Ref. [125], under these conditions the elusive Risken-Nummedal-Graham-Haken (RNGH)-like instability can be observed in QCLs. It is demonstrated that fast gain recovery of QCLs exhibits two kinds of instabilities in the multi-mode regime: the RNGH-like instability and one associated with spatial hole burning (SHB) [126].
The active mode locking in QCLs is strongly limited by SHB which leads to a proliferation of modes with random phases and destroys coherence [191].
In this chapter we investigate performance optimization and passive mode locking caused by a saturable absorber in a ring cavity QCL in which the SHB instability does not occur because of the absence of standing waves. Performance optimization of QCLs has achieved significant progress in recent years [192, 193, 104]. The performance of QCLs can be improved by optimizing the epitaxial growth, fabrication process, and active region design [194, 195, 196]. The latter is important in order to insure efficient carrier injection in the upper lasing state and carrier extraction out of the lower lasing state [104].
So far, optimization techniques proposed to design QCL structures are based on genetic algorithms [104, 192, 197, 198]. A multi-variable multi-objective optimization algorithm for terahertz QCLs is presented in [193]. In [104, 192], a technique to design quantum cascade structures in the mid-infrared is proposed. Particle swarm optimization (PSO) [199] is as an alternative to traditional evolutionary algorithms. It attempts to mimic the goal-seeking behavior of biological swarms. In PSO, a possible solution of the optimization problem is represented as a particle, and the algorithm operates in an iterative manner. Unlike traditional evolutionary algorithms, particles in PSO do not perform the operation of genetic recombination between particles, but they work individually with social behavior in swarms. PSO has some attractive characteristics. In particular, it has memories, so that knowledge of good solutions can be retained by all particles (solutions). This method has been successfully used to solve many discontinuous and complex problems with good results [200, 201].
We perform an optimization study of ring cavity QCLs considering the laser instability condition. Laser design parameters, including the barrier and well thicknesses and applied electric field, are modified for maximizing laser gain under a desired instability condition. Passive mode locking with saturable absorber is investigated for the optimized QCLs. The effects of saturable absorber and pumping strength on the instability characteristics are studied. A large optical gain below the instability threshold is achieved for optimized QCL designs. A numerical calculation based on the Maxwell-Bloch equations is performed to analyze the optimized structure.
Because of the large number of involved design parameters, performance improvement of QCLs requires a systematic multi-objective optimizer in conjunction with a simulation tool which has a good balance between computational speed and physical accuracy.
Various approaches such as rate equations [202, 203], Monte-Carlo simulations [204], density matrix methods [205], and the non-equilibrium Green’s function formalism (NEGF) [206, 207] have been developed for the simulation of QCLs.
The simplest models, based entirely on scattering and neglecting coherence effects, require a fewer number of material parameters and are generally able to predict the threshold current density but not the light-current or current-voltage characteristics [208]. Pure quantum mechanical models based on NEGF or the density matrix have been used as rigorous approaches to capture the QCL physics. The NEGF theory takes into account incoherent scattering with phonons, impurities, and rough interfaces as well as electron-electron scattering in the Hartree approximation [206]. Unfortunately, the inherently high computational costs of the full quantum mechanical models render them unfeasible for optimization purposes [206].
To study electronic transport in QCL, we employ the Pauli-master equation solved by the Monte-Carlo method [209]. In this semi-classical approach, the transport is modeled via scattering between energy states, including acoustic and optical deformation potential and polar optical electron-phonon scattering as well as alloy, inter-valley, and interface roughness scattering. Accurate results along with a relatively low computational cost render this approach as a good candidate for optimization studies.
Although quantum cascade structures (QCSs) have a long history, many aspects of the carrier transport and interaction with light field are still unclear. Very important question concerning physics of the QCSs is whether transport is coherent or incoherent. There were many discussions about the problem, and several attempts to estimate the kind of transport were successful, especially [210, 211]. The answer on this question depends on conditions of QCSs operation. For example, the coherent electron transport is of interest in the non-equilibrium regime at femtosecond and picosecond time intervals. The incoherent transport is prevalent at the high excitation level in the stationary quasi-equilibrium regime. In both cases, the electronic transport influences the optical properties of the device. In this connection, the development of the theory for coherent and incoherent electron transport regimes, included many-body effects and light-matter interactions in QCS, is of actual interest. We employed the Pauli master equation [212] to model current transport through the QCL semiconductor heterostructure. Based on the experiences of a MATLAB prototype presented in [204], an optimized Monte Carlo (MC) simulator has been implemented in C++ within the Vienna-Schrödinger-Poisson (VSP) simulation framework [213, 214].
In many practical cases the steady state transport in QCLs is incoherent such that a semiclassical description can be employed [210, 215]. Following this approach, a transport simulator for quantum cascade lasers based on the Pauli master equation [204] has been developed. The transport is described via scattering transitions among quasistationary basis states which are determined by numerically solving the Schrödinger equation. The Hamiltonian includes the band edge formed by the heterostructure. In this way, tunneling is accounted for through the delocalized eigenstates. The transport equations are derived from the Liouville von Neumann equation in the Markov limit in combination with the diagonal approximation. This means that the off-diagonal elements of the density matrix are neglected and one arrives at the Boltzmann-like Pauli master equation [216]
| = |
| Smn(k′,k)fk,n(t) −Snm(k,k′)fk,n(t) . (1) |
Here, m and n denote the subband indices, and k and k′ the in-plane wave vectors. The transition rate from state | k′,m⟩ to state | k,n⟩ for an interaction Hint follows from Fermi’s golden rule
| Snm(k,k′))= |
| |⟨ k′,m| Hint| k,n⟩| 2 δ (ε(k′)−ε(k)∓ℏω) (2) |
The simulator makes use of the translational invariance of the QCL structure and simulate the electron transport over a single stage only [217]. The wave function overlap between the central stage and spatially remote stages is small. It is therefore assumed that interstage scattering is limited only to the nearest neighbor stages and that interactions between basis states of remote stages can be safely neglected. The states of the whole QCL device structure are assumed to be a periodic repetition of the states of a central stage. This approach ensures charge conservation and allows imposing periodic boundary conditions on the Pauli master equation. Since transport is simulated over a central stage only, every time a carrier undergoes an interstage scattering process the electron is reinjected into the central stage with an energy changed by the voltage drop over a single period. The total current is determined by the net number of interstage transitions. The transport equations is solved using a Monte Carlo approach. Several new numerical methods are employed to reduce the computational cost of the simulation [209].
The PSO is an iterative method which initializes a number of vectors (called particles) randomly within the search space of the objective function. The set of particles is known as the swarm. Each particle represents a potential solution to the problem expressed by the objective function. During each time step the objective function is evaluated to establish the fitness of each particle using its position as input. Fitness values are used to determine which positions in the search space are better than others. Particles are then made to fly through the search space being attracted to both their personal best position as well as the best position found by the swarm so far [218]. The particles are flown through the search space by updating the position of the ith particle at time step k according to the following equation [218]:
| xik+1 = xik + vik, (3) |
where xik and vik are vectors representing the current position and velocity, respectively. Assuming vectors of dimension, the updates of the jth velocity component is governed by the following equation [219]
| (4) |
where 0 < ω < 1 is an inertia weight determining how much of the particle’s previous velocity is preserved, c1 and c2 are two positive acceleration constants, r1,j and r2,j are two uniform random sequences sampled from U(0, l), yi is the personal best position found by the ith particle and ŷ is the best position found by the entire swarm so far. The following relation should hold in order for the PSO to converge [218]:
| −1 < ω. (5) |
However, the standard PSO is not guaranteed to converge on a local extremum, but most of the recent PSO algorithms converge to the global optimum.
Employing a Pauli master equation-based description of electronic transport in QCLs along with the multi-objective PSO strategy, a framework is developed for maximizing laser gain with simultaneous desirable instability operation. In this framework one starts from a reference design. In the next iterations the well and barrier thicknesses and the applied electric field are modified until maximum gain and laser operation below the instability threshold are achieved. The analytical linear stability model introduced in Ref. [126] is employed to analyze the instability threshold of the studied QCL. In this model, the criteria for the RNGH instability is expressed in terms of the parametric gain g(Ω) as a function of the resonance frequency Ω
| (6) |
where pf is the pumping factor, T1 is the gain recovery time, T2 is the dephasing time, l0 is the linear cavity loss, µ is the matrix element of the lasing transition, and γ is the SA coefficient. The derivation of Eq.6 is presented in detail in Appendix C. Based on this analysis, each mode which is identified by the resonance frequency Ω, is stable if the parametric gain is negative, otherwise it is unstable. At each iteration of the optimization loop, for a set of geometrical parameters and the applied electric field, the parameters T1 and µ are extracted and the parametric gain (Eq. 6) is evaluated. The parameter T2, dephasing time, can be approximated by T1/10 as mentioned in [220]. If the stability condition is not satisfied, a new set of parameters is selected for the next iteration. The flow chart of the developed framework is described in Fig. 6.1.
We consider the laser gain as a figure of merit and define the instability criterion to satisfy stability conditions. Using the scattering times and calculating the dipole matrix elements, the gain coefficient g can be estimated for each structure as [108]:
| g = τ3 | ⎛ ⎜ ⎜ ⎝ | 1− |
| ⎞ ⎟ ⎟ ⎠ |
|
| , (7) |
where λ0 is the wavelength in vacuum, є0 the vacuum dielectric constant, e the elementary charge, neff the effective refractive index of the mode, Lp the length of one period including active region and injector, and 2γ32 is the full width at half maximum value of the luminescence spectrum.
In fact, the optimization framework changes the geometrical parameters which affect the lifetimes and matrix elements. Simulation results indicate that the two key parameters to be optimized are the matrix element µ and the upper laser level lifetime τ3 (≈ T1 in Eq. 6). The gain coefficient increases with these two parameters (see Eq. 7). The reference design has a 3QW vertical active-region. The parameters of the reference design are mentioned in [221]. The layer sequence of the In0.52Al0.48As/In0.53Ga0.47As heterostructure for the optimized design, starting with the injection barrier is: 3.74/2.36/1.50/7.45/1.63/5.63/2.15/4.43/3.86/3.85/ 3.15/3.18/4.40/2.79/2.67/2.46 nm, where the barrier layers are in bold and underlined layers are n-doped with Si at 2 × 1017 cm−3.
Figure 6.2(a) shows the PSO results for different particles in the search space. Most of the points (samples) are located at the right-side of the vertical dashed-line which represents unstable laser operation. The samples at the left-side of the vertical dashed-line and above the horizontal dashed-line are the ones we are looking for.
The instability threshold behavior and gain spectrum for the reference design and two obtained optimized designs are exhibited in Fig. 6.2(b). The first structure is optimized at the same wavelength as the reference design and the second one is optimized at a higher wavelength but with a larger gain. Our developed framework has the advantage of optimizing the reference structure for a specific wavelength. We focus on the first optimized structure which has the same wavelength as the reference structure.
The conduction band diagram and the associated wave-functions of the reference design and optimized structure are shown in Fig. 6.3. The active region of the optimized structure is a three-well (3QW) vertical-transition design which provides high optical gain and concomitant robustness for laser action, see Fig. 6.3(b). The upper laser level for the optimized structure is delocalized which results in an increase of the upper laser level lifetime τ3 and consequently the laser gain, see Eq. 7.
Table 6.1: The parameters used for the instability analysis of the optimized structure.
T1 Gain recovery time 0.46ps T2 Dephasing time 0.06 ps µ Matrix element of lasing transition 2.44× 10−9 m n Refractive index 3.25 l0 Linear cavity loss 500 m−1 L Cavity length 6× 10−3 m γ Saturable absorber coefficient 10−11m/V2
The parameters extracted for the instability analysis of the optimized structure are shown in Table 6.1. Fig. 6.4(a) indicates that the instability threshold decreases uniformly with the SA coefficient, for example γ ≥ 3 m/V2 triggers the instability for the optimized structure at a relatively low pumping strength (pf=2). As reported in [126], a saturable absorber always favours a multimode regime to a single mode one, which explains why the instability threshold decreases with γ in the optimized design. As discussed later, this instability results in Rabi sidebands around the cw lasing frequency.
The parametric gain of the optimized structure at various pumping strengths is shown in Fig. 6.4(b). A larger pumping strength broadens the instability characteristics and decreases the instability threshold. The results are consistent with previous works [126].
Next, we present the optimization results for a reference QCL with a superlattice (SL) active-region [105].
The layer sequence of the SL structure, starting with the injection barrier, is as follows:
4.0/1.9/0.7/5.8/0.9/
5.7/0.9/5/2.2/3.4/1.4/3.3/ 1.3/3.2/1.5/
3.1/
1.9/3.0/
2.3/2.9/2.5/2.9 nm.
The In0.52Al0.48As barrier layers are in bold and In0.53Ga0.47As well layers are in roman. The underlined layers are n-doped with Si at 4×1017cm−3.
The instability characteristics for the 3QW and SL active-regions are compared in Fig. 6.5(a). Because of the larger matrix element (µ) and longer upper laser state lifetime (τ3), which is approximately equal to the gain recovery time (T1), the SL active-region QCL indicates more stable operation and higher instability threshold, see Fig. 6.5(a). However, as we mentioned earlier, the matrix element and lifetimes of the lasing transition, which are the key parameters in linear stability analysis, are proportional to optical gain (see Eq. 7). As indicated in the inset of Fig. 6.5(b), the 3QW QCL exhibits larger optical gain at nearly the same wavelength. The optical gain of the 3QW structure is maximized by delocalizing the lasing states which increases the lifetimes τ3 and τ2. Because of the bound states in the SL active-region, there is no significant lifetime variation, however, due to the larger matrix element, a better instability condition is achieved.
Terahertz frequencies (1-10 THz, 30-300 µm) are among the least developed electromagnetic spectra even though they have wide ranging applications in spectroscopy, imaging, and remote sensing [222]. Since the report of quantum cascade lasers (QCLs) operating in the terahertz spectral region by Köhler et al. [99] there has been significant progress concerning the available frequencies, the temperature performance, and the understanding of the dynamics [223].
Emitting radiation due to intersubband optical transitions in QCLs makes this possibility to generate terahertz radiation in these lasers. The terahertz radiation in QCLs could be engineered by electronic bandstructure. We select the designs that utilize strong electron-phonon interaction in the semiconductor as a means to establish population inversion for optical gain [2].
Based on the algorithm introduced in Sec. 6.1.2, we study the SA and pumping factor effects on instability characteristics of terahertz QCLs.
Here, a reference QCL operating at 3.44 THz, corresponding to λ = 87.2 µ m, is employed [4]. The layer sequence of the reference structure, starting with the injection barrier, is as follows: 5.4/7.8/2.4/6.43.8/14.8/2.4/9.4 nm. The 14.8 nm well is doped at 1.9×1016cm−3. The operating temperature for reference design is 5 K up to 65 K, however, higher operating temperatures are achieved for optimized THz QCLs.
Figure 6.6 exhibits instability characteristics for two QCLs operating in infrared and terahertz spectral region. Figure 6.6(a) indicates that the instability threshold decreases faster with SA coefficient for mid infrared QCL sample while the terahertz QCL sample still operates below the instability threshold. SA can bring g(Ω) above zero, thereby triggering an instability which is more effective for mid infrared QCL. The parametric gain of the optimized structure at various pumping strengths is shown in Fig. 6.6(b). A larger pumping strength broadens the instability characteristics and decreases the instability threshold which is significant for mid infrared QCL. The results indicate more stability for QCLs operating in the terahertz spectral region.
The linear stability analysis, however, predicts only the instability threshold and does not describe the dynamics of the laser. To investigate the dynamics of QCLs above the instability threshold, the Maxwell-Bloch equations are solved numerically. The effect of the SA is modeled as the intensity-modulated optical field amplitude in the standard Maxwell-Bloch equations[128]:
|
E and P are the envelopes of the normalized electric field and polarization, respectively, D represents the normalized average population inversion, Dp is the normalized steady-state population inversion, Dth is the lasing threshold value of Dp for γ=0, proportional to the pumping factor pf (pf≥ 1), l0 is the linear cavity loss, and γ=ℏ2γ/µ2.
We employ a finite-difference discretization scheme to find the evolution of electric field, polarization, and population inversion in the spatial and time domain. A periodic boundary condition is applied to model a ring cavity. The equations are discretized to calculate the state of the system in each step from the state in the previous step. This procedure is shown in Fig. 6.7.
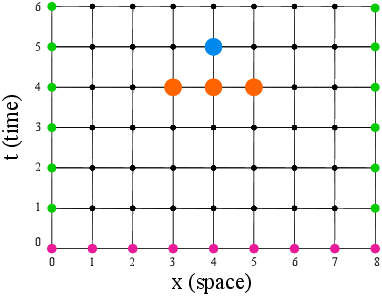
Figure 6.7: The m× n mesh points for the finite difference approximation. Here m=8 and n=6. The boundary conditions are shown by green dots and initial condition by pink dots. E(m,n+1), a sample step in time domain, is shown with blue dot and its value is dependent on the previous steps, the orange dots.
The number of mesh points play an important role in preventing unreasonable results and achieving consistency. The number should be large enough to make sure there is not any un-inspected variation. The x−t plane is divided into a m× n mesh points as shown in Fig. 6.7. The number of mesh points are m=500 and n=105 which correspond to the grid sizes of Δ x=L/m=12 µm and Δ t=Δ x/c=120 fs. The periodic boundary conditions for the dynamical variables of the QCL (electric field E, polarization P, and population inversion D) are E(0,n)=E(L,n), P(0,n)=P(L,n), and D(0,n)=D(L,n).
The derivatives of variables in time and space are achieved by Taylor expansion about the grid point (m,n). ∂_tE(m,n) = -E(m,n+1)-E(m,n)/Δt-1/2Δt∂^2E(m,n)/∂t^2 ∂_zE(m,n) = -E(m,n)-E(m,n-1)/Δz+1/2Δx∂^2E(m,n)/∂z^2 Similar expressions are written for ∂tP and ∂tD. Starting with the left hand-side of Eq. 6.3 and 6.3 for the electric field, we have
Ė+c∂E/∂z =-E(m,n+1)-E(m,n)/Δt-1/2Δt∂^2E(m,n)/∂t^2
-E(m,n)-E(m,n-1)/Δz+1/2c^2 Δt^2∂^2E(m,n)/∂z^2=
E(m,n+1)-E(m-1,n)/Δt+1/2Δt [c^2∂E(m,n)/∂z^2-∂E(m,n)/∂t^2]
=k(P-E).
The expression Ė denotes ∂tE.
Selecting the second equality helps to eliminate the terms with first derivative
k(P-E) = E(m,n+1)-E(m-1,n)/Δt
+1/2Δt [c^2∂^2E(m,n)/∂x^2-∂^2E(m,n)/∂t^2]
Solving Eq.6.3 for E(m,n+1) gives
|
In this way, we have approximated the derivatives up to the order Δ t2.
From Eq. 6 we have
|
|
If we multiply Eq. 8 by c2 and then subtract it from Eq. 7
|
As
|
and
|
the right side of the Eq. 9 can be simplified to
|
where we used the following relationship for the speed of wave propagation in vacuum
|
Therefore, evolution of electric field in time and space is given by
|
rearranging the equation results in:
|
Following a similar procedure, the equations for P and D are obtained. The details and the full derivations of this method can be found in [224].
Because we have neglected noise in our treatment, the solutions would remain | E |=| P |=0 for all times. In order to get the laser started, one must therefore assume a small initial disturbance of the electric field, e.g., a Gaussian [224]
|
The initial inversion D is set to the threshold pumping pf which is the minimum injection current needed to start the lasing action.
|
Figure 6.8 indicates the transient buildup of the intensity for a ring cavity without the saturable absorber effect. After a few round trips, E,P, and D reach the approximate periodic steady state. To investigate the saturable absorber effect, we recalculate the variables including the saturable absorber term in the Maxwell-Bloch equations, see Eq. 8.
For the parameters corresponding to the optimized 3QW QCL including the SA, the lasing instability appears as the rise of the side modes with the increase of the SA coefficient. The energy in the Rabi sidebands can change either discontinuously or continuously at the RNGH instability threshold[126]. In lasers with slow gain recovery time, the transition in the Rabi sidebands is discontinuous [225], however, because of the fast gain recovery time in QCLs, Rabi sidebands continuously grow around the central cw mode, see Fig. 6.9. Furthermore, more Rabi side modes appear with the increase of the pumping strength.
Intersubband (ISB) photodetectors, demonstrated in 1987 in the form of photoconductive quantum-well infrared photodetectors [226], has attracted much scientific attention in recent years. Particularly at the energetic extremes of infrared radiation, namely in the low energy THz and in the high-energy near-infrared ranges, there are still challenges in finding suitable materials and designs for ISB photodetectors [227].
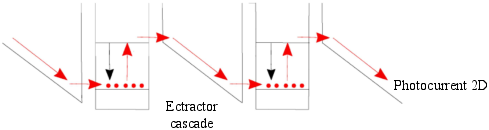
Figure 6.10: Schematic conduction-band diagram of a QCD. Ground-level electrons are excited to the active QW’s upper level by absorbing a photon. Due to the asymmetric band profile between two active QWs, the cascade excited electrons relax mostly in one direction (in this case to the right), resulting in a net photocurrent. Adapted from [227].
In the NIR, fast intraband semiconductor photodetectors are only available for wavelengths up to about 1.6 µ m. For the other end of optical spectrum, namely for detection of THz radiation, bolometers are widely used; however, they are not well suited for high-speed applications. ISB photodetectors can be designed for a wide range of wavelengths in a single material system just by choosing adequate semiconductor layer thicknesses [227]. This advantage of ISB photodetectors make them very promising candidates for THz radiation. Compared with photoconductive ISB photodetectors, the research on zero-bias photovoltaic ISB photodetectors has seen less progress. Schneider et al. [228, 229] observed pronounced photovoltaic effects in an asymmetric multi-QW structure. According to Schneider [230], an optimized photovoltaic photodetector has superior noise properties, the capability to operate at higher photon fluxes, and an improved dynamical range.
Hofstetter et al. [231] used a QCL structure as photovoltaic detector which is employed as a prototype device in this section. In analogy to the functioning of a QCL, a similar but optimized ISB detector presented by Gendron et al. [232] was named quantum cascade detector (QCD). QCDs offer more design freedom for a given material composition.
The operating principle of a QCD is outlined in Fig. 6.10. A ground level electron is excited to a higher state by absorbing a photon. Due to the asymmetric design, the electron relaxes in a preferred direction into the quantum well of the next cascade. This concept reduces dark current and dark current noise.
We have developed the QCL optimization algorithm to maximize the performance of QCDs. The QCD device N1022 reported in [227] is selected as the reference design. The layer sequence of the In0.53Al0.47As/In0.53Ga0.47As QCD structure, starting with the well, is as follows: 5.1/7.5/1.25/6.5/1.45/6.4/1.7/7.9/2.0/7.7/2.4/7.5/2.9/7.1/3.5/6.8 nm. The underlined layer is n-doped with Si at 4×1017cm−3.
The responsivity at the room temperature is selected as the figure of merit. The wavelength operation of the optimized structures are set to be the same as the wavelength of the reference design. The optimization results for the responsivity is presented in Fig. 6.11. Larger responsivities are achieved for optimized QCD structures. However, for larger responsivities the bandwidths of optimized QCDs are increased. The results indicate the excellent performance of our developed optimizer for QCDs.


