


Chapter 5 Graphene Superlattice-Based Photodetectors
Superlattices and various quantum structures obtained thereof have drawn much attention in past decades [46]. Commensurate or pseudomorphic junctions of two different semiconductors have been grown layer by layer to form a periodically repeating superlattice structure with sharp lattice-matched interface [96, 174, 175]. Owing to the band discontinuities at the interface, they behave as a multiple quantum well structure according to the effective mass theory. Electrons confined in these quantum wells exhibit two-dimensional electron-gas behavior with interesting quantum effects [46]. Two-dimensional conduction-band electrons (valence-band holes) confined to the wells have displayed a number of electronic and optical properties [96, 174, 175, 176, 177].
In this chapter, the optical properties of hydrogen-passivated armchair graphene nanoribbons superlattices (HSLs) and boron-nitride-passivated armchair graphene nanoribbons superlattices (BNSLs) are studied.
The results indicate high responsivity and quantum efficiency as well as long wavelength operation
which render these devices as potential candidates for future photodetection applications.
Figure 5.1 shows the structure of the studied superlattices. In the structure shown in Fig. 5.1(a) the dangling bonds of edge carbon atoms are saturated by hydrogen atoms, whereas in the structure shown in Fig. 5.1(b) the semiconducting region (formed by carbon atoms) is surrounded by BN. Throughout this study, the structures in Fig. 5.1(a) and (b) are used as main structures which are referred to as HSL(11) and BNSL(11), respectively. The numbers inside the parentheses represent the number of carbon atoms along the width of the wider part of the superlattice (nw).
Lengths of 8acc and 7acc are considered for the well and barrier regions, respectively, where acc=1.42 Å is the carbon-carbon bonding distance.
To investigate the optical properties of these superlattice structures, the non-equilibrium Green’s function (NEGF) formalism introduced in Sec. 3.1.3 along with a tight-binding (TB) model for the electronic bandstructure (Sec. 3.1.2) are employed. The TB parameters are modified to match the results with first principle calculations.
For first principle calculations we employed the SIESTA package [152]. The parameters used for the DFT calculation are given in Sec.3.1.1.
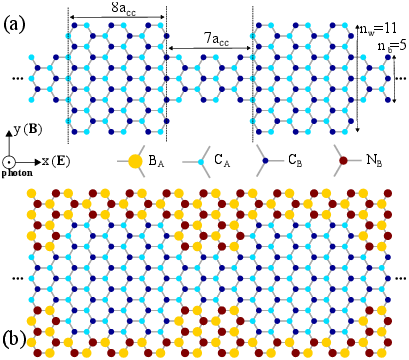
| Figure 5.1: The structure of (a) a hydrogen-passivated superlattice, and (b) a boron nitride-confined superlattice. Both superlattices have the same index for the graphene nanoribbon part. CA/B represents a carbon, NA/B a nitrogen, and BA/B a boron atom at the sublattice A or B. nw and nb denote the well and barrier indices respectively. |
5.1 Graphene Superlattice Properties
| Table 5.1: The proposed TB model parameters for the superlattice. All parameters are expressed in electron volt. |
|
|
| tCC | tBB | tNN | tBC | tNC | tBN |
|
| 2.35 | 0 | 0.45 | 2.1 | 2.4 | 2.8 |
|
|
| tCC,2 | tBC,2 | tNC,2 | △CC | △BB | △NN |
|
| 0 | 0.1 | 0.3 | 0.015 | 2.05 | -2.05 |
|
Figure 5.2 compares the bandstructures for HSL(11) and BNSL(11) based on the TB model and first principles calculations. Carbon-carbon interactions up to three nearest neighbors are considered in the TB calculations for HSLs. In the case of BNSLs, a more careful choice of the TB parameters is required due to the ionicities of the boron and nitrogen atoms at the edges of the superlattice. The tight-binding parameters proposed in Table 5.1 result in electronic disperse relations that are in excellent agreement with first-principle simulations.
In this table, tXY and tXY,2 denote the hopping parameter between the first and second nearest neighbor X and Y atoms, where X and Y represent carbon C, boron B, or nitrogen N atoms. ΔXX denotes the on-site potential of atom X.
As shown in Fig. 5.2(a), larger energy gaps are achieved for BNSLs in comparison with HSLs, which is attributed to the large ionic potential difference between boron and nitrogen atoms in BNSLs [135].
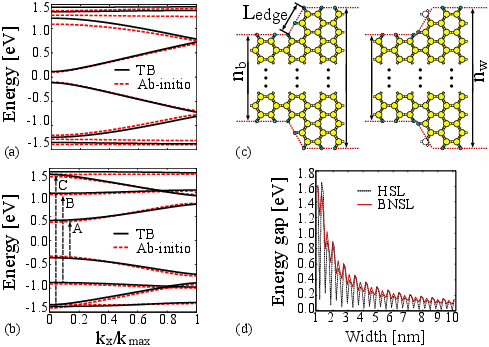
| Figure 5.2: The electronic bandstructure for (a) a HSL(11), and (b) a BNSL(11) based on the TB model and first principles calculations. (c) The geometrical parameters of the structure. (d) Energy gap as a function of nw for a HSL and a BNSL. |
The bandgap as a function of the width of superlattice is depicted in Fig. 5.2(d).
Zigzag edges in a graphene layer induce an opposite spin orientation across the ribbon
between ferromagnetically ordered edge state [178]. In such cases, additional spin analysis
is necessary which is beyond the scope of this work.
To avoid zigzag edges, we assumed that nw and nb are scaled such that Ledge is kept constant, where nw and nb are defined as the number of dimer lines in the well and barrier of the superlattice, respectively, see Fig. 5.2(c). Figure 5.2(d) shows that HSLs, unlike BNSLs, have relatively small bandgap for specific values of nw=3p+2, where p is a positive integer. In addition, the scaling of the energy gap with the width in BNSLs shows a more uniform behavior compared to that of HSLs. An important point to notice is the instability of the superlattice shown in the right side of Fig. 5.2(c) as a result of the dangling bonds, which will quickly relax to form another geometry. In fact, all superlattices with even values of nw are unphysical, and thus the studies are restricted to odd values of nw.
The optical response of the superlattices presented in Fig. 5.1 is studied in terms of the interband dielectric response function (Eq.4). The details of dielectric response function is presented in Sec. 3.1.1.
[capbesideposition=right,center]figure[]
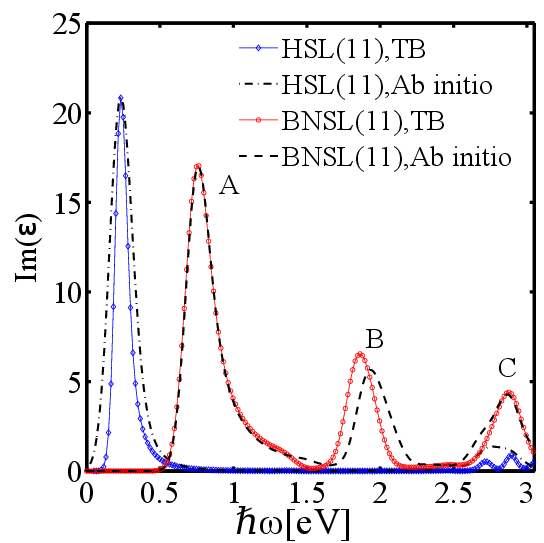
| Figure 5.3: The dielectric response of a HSL(11) and a BNSL(11) based on the TB (solid lines) and first principles calculations (dashed lines). The optical power density is 100 kW/cm2 and the photon flux is assumed to be normal to the
HSL/BNSL plane. |
Figure 5.3 compares the imaginary parts of the dielectric functions for a HSL(11) and a BNSL(11). The absorption spectrum exhibits its first peak at ℏω=0.33eV which corresponds to a transition from the highest valence band to the lowest conduction band. The optical absorption spectrum of BNSL(11) exhibits additional peaks in the photon energy range 0<ℏω<3.5eV. The absorption peaks occur at the photon energies of 0.91eV, 1.965eV, and 3.156eV which are related to transitions represented by A, B, and C in Fig. 5.2(b), respectively. The comparison of the dielectric functions in Fig. 5.3 with the bandstructures shown in Figs. 5.2(a) and (b) suggests that for this specific structure only transitions from valence bands to conduction bands with the same index are allowed. This, however, is not a general transition rule for BNSLs and does not hold at various geometrical parameters.
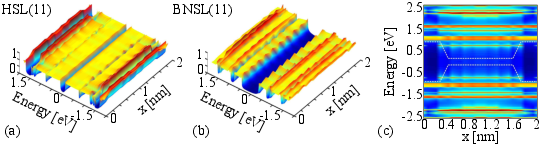
| Figure 5.4: The local density of states for (a) an HSL(11) and (b) a BNSL(11). (c) normalized LDOS for a unit cell of an ultrathin HSL. The optical power density of 102 kW/cm2 and the photon flux normal to the
HSL/BNSL plane are assumed. |
In order to get a deeper understanding on the operation of such structures the local density of states (LDOS) and photocurrent need to be carefully considered. Figures 5.4(a) and 5.4(b) show
the LDOS for the superlattices under study. These LDOS plots indicate the presence of localized states in both structures. The normalized LDOS for the unit cell of an ultrathin HSL is shown in Fig. 5.4(c). It is predictable that the first peak in the optical spectrum occurs at ℏω=1.5eV which is related to an optical transition between the two confined states at energies 0.74eV and 0.69eV (See Fig. 5.4(c)). Since the presence of these two states is forbidden in the barrier regions of the superlattice, the photocurrent at ℏω=1.5eV is completely of quantum mechanical nature. At higher energies some continuous minibands are formed which give rise to the photocurrent observed at approximately ℏω=2eV.
In order to assess the performance of superlatice structures for photodetection applications, the quantum efficiency and the photoresponsivity of the presented structures are evaluated. The quantum efficiency is defined as α =(Iph/q)/(Pop/ℏω), where Iph and Pop are the photocurrent and the incident optical power, respectively. Figure 5.5(a) and (b) shows the calculated photocurrent and quantum efficiency as a function of the incident photon energy, respectively, for HSL(11) and BNSL(11). The quantum efficiency peaks if the photon energy corresponds to an allowed intersubband optical transition. The quantum efficiency of the HSL reaches the values of about 20%, which is significantly larger than that of H-AGNRs [171]. For the case of BNSL(11), there are more peaks in the specified energy range due to the different subband spacings in comparison with that of HSL(11). Quantum efficiencies of 13% and larger than 20% are obtained for the first and second peaks in the optical spectrum, respectively. The photoresponsivities- defined as Iph/Pop- of HSL and BNSL reach 0.866A/W and 0.303 A/W, respectively, where the optical power is assumed to be 100 kW/cm2.
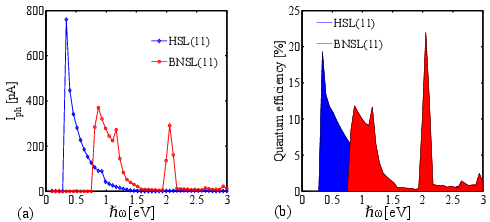
| Figure 5.5: (a) Photocurrent and (b) quantum efficiency for a HSL(11) and a BNSL(11). The optical power density is 100 kW/cm2 and the photon flux is assumed to be normal to the
HSL/BNSL plane. |
In this study, a small voltage bias in the range of 0.05-0.1V is applied to drive the generated electrons and holes towards the contacts. The restriction for the applied voltage bias is the band to band tunneling which
increases the dark current and is detrimental for photodetectors. The tunneling current has an exponential dependence on the electric field. Due to the relatively small length of proposed superlattice photodetectors, applying even a small voltage bias may cause a huge electric field. For example a voltage bias of 0.1V leads to an electric field of 4.7×105V/cm.
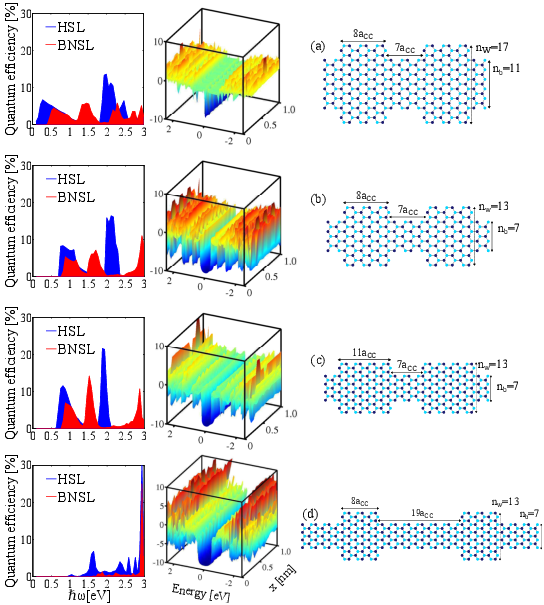
| Figure 5.6: The structure of (a) HSL(13) and (b) HSL(17). (c,d) Superlattices with different well/barrier lengths. The quantum efficiency and local density of states of each structure are depicted. |
The structural parameters effects on superlattice photodetector characteristics are examined.
Figures 5.6(a) and 5.6(b) indicate that more peaks appear in the quantum efficiencies of HSL/BNSL(13) and HSL/BNSL(17) compared to the main structure (Fig.5.5(b)). If the width of the superlattice increases, energy gaps decrease which allow more optical transitions. This behavior is similar to that of GNRs [179], however, in superlattice photodetectors, the quantum efficiencies at higher energies are larger in comparison with that of lower energies. This is due to the presence of barriers that block transport of photo-generated carriers which is more pronounced by increasing the barrier/well lengths, see Fig. 5.6(c) and Fig. 5.6(d). It should be noted that the confinement due to the presence of barriers only weakly affects devices with relatively long wells and the characteristics of such structures become similar to conventional GNR-photodetectors.
5.2 Line-edge Roughness Effects
Line-edge roughness plays an important role on the characteristics of narrow GNRs. Experimental data show that line-edge roughness is the dominant scattering mechanism for GNRs narrower than 60nm [180]. Line-edge roughness causes fluctuations in the edge potential and leads to the modulation of the energy gaps which affects optical transitions and photon absorption energies. Therefore, a careful investigation of this effect on the optical properties of GNR superlattices is essential. Line-edge roughness is a statistical phenomenon that can be well described by means of an exponential autocorrelation function [179]:
|
R(x)=Δ W2 exp | ⎛
⎜
⎜
⎝ | − | | ⎞
⎟
⎟
⎠ | ,
(1) |
where Δ L is the roughness correlation length which is a measure of smoothness and Δ W is the root mean square of the fluctuation amplitude. To create line-edge roughness in real space, a random phase is added to the Fourier transform of the autocorrelation function (power spectrum) followed by an inverse Fourier transform [181]. Using the obtained roughness profiles various devices are generated. The optical characteristics of each device is evaluated separately, followed by an ensemble average.
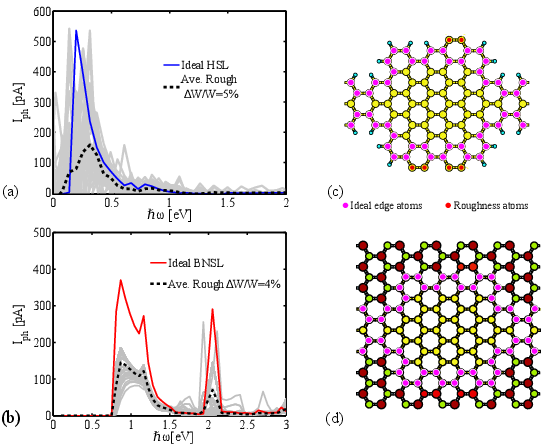
| Figure 5.7: (Dashed-black line) The average photocurrent spectrum over different samples and (gray lines) the photocurrent spectrum of each sample as a function of the incident photon energy.(a,c) HSL and (b,d) BNSL. |
The effect of line-edge roughness on the electronic properties of GNRs has been investigated in several analytical [179, 182] and numerical studies [183, 184]. Here, we investigate the role of roughness on the spectrum of photocurrent in GNR-based superlattices.
We add/remove an integer number of atoms from the edges based on their relative position with respect to the generated rough edge. However, this may result in an unstable edge-structures with monomers instead of dimers at the edges. In these cases, the edges are reconstructed to be physically stable.
For the given geometrical and roughness parameters many samples are statistically generated.
The characteristics of each device is evaluated followed by an ensemble average over all samples, see Fig. 5.7.
More details about our approach can be found in [181].
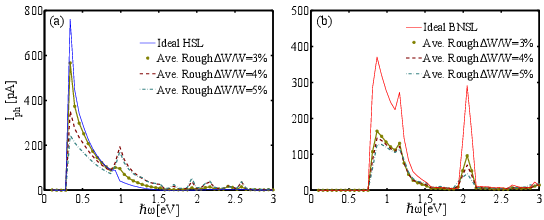
| Figure 5.8: The ideal and average photocurrent spectra for (a) HSL(11) and (b) BNSL(11) at various roughness amplitudes. |
Due to backscattering of carriers, the photocurrent and quantum efficiencies of both supper lattices decrease in the presence of line-edge roughness. Figure 5.7 shows that due to effective width variation, the photoabsorption peaks appear at energies larger or smaller than the peaks of the structure without disorder. The average width of edge-defected devices, however, is equal to that of a device with perfect edges. Therefore, line-edge roughness does not affect the location of the average photocurrent peak.
Figure 5.8 exhibits the results for HSL(11) and BNSL(11) with edge disorders.
Roughness is expressed in terms of nw because the well has a more significant
effect on the optical transitions. The absolute roughness amplitude is the same all over the device.
In the case of BNSL(11), the roughness is applied at the C-BN interfaces. As it is shown in Fig. 5.1,
a BN passivation with 2/3 dimers is considered in BNSLs. For the roughness amplitudes of 3%,4%, and 5%,
the structures are still passivated with BN. However, for larger roughness amplitudes
the roughness may cross the boundaries without any BN passivation. In these cases,
the structures are reconstructed by additional BN dimmers at the boundaries.
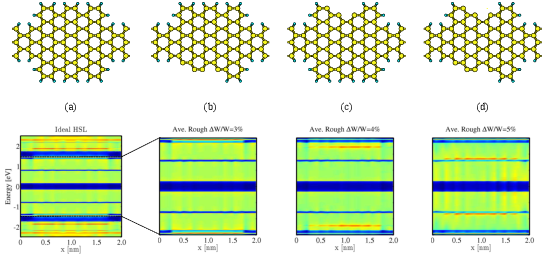
| Figure 5.9: Local density of states for (a) an ideal and (b,c,d) rough HSL(11) at various roughness amplitudes. The optical power density is 100 kW/cm2 and the photon flux is assumed to be normal to the
HSL/BNSL plane. |
HSL(11) exhibits photoresponsivity and quantum efficiency reductions of 23%, 55%, and 70% for the relative roughness amplitudes of 3%, 4%, and 5%, respectively, whereas a smoother behavior is observed for BNSL(11) (compare Fig. 5.8(a) and (b)). This behavior is attributed to the stable configuration of edge-carbon atoms in BNSL in comparison with HSL in the presence of line-edge roughness.
The average photocurrent of edge-defected HSLs peaks at photon energies around ℏω=1eV. This peak is related to line-edge roughness induced states, see Fig. 5.9. Due to the formation of dangling bonds in the presence of line-edge roughness, these states are formed. As the relative roughness amplitude increases more states are induced and more photocurrent is generated by transitions from these states. However, dangling bonds are absent in edge-defected BNSLs and such states do not appear in such structures.
black
5.3 Conclusions
The optical properties of graphene nanoribbon superlattices embedded in boron nitride sheets and the possibility of using such structures as photodetectors are studied. We propose a set of tight-binding parameters for the investigated structures which shows excellent agreement with first-principles results. The results indicate that the optical spectrum of a BN-confined AGNR superlattice contains more absorption peaks and show more optical intersubband transitions compared to a hydrogen passivated superlattice with the same geometry. Employing the non-equilibrium Green’s function method, the photocurrents and quantum efficiencies are evaluated and compared for both devices at various incident photon energies.
Using an statistical approach the role of line-edge roughness on the optical properties of GNR-based superlattices is investigated. The results indicate that the quantum efficiency and photoresponsivity decrease in the presence of line-edge roughness.
For HSL, induced states appear and increase with the roughness amplitude which result in the appearance of an additional peak in photocurrent spectrum. In comparison with HSLs, BNSL photodetectors exhibit more robust optical properties in the presence of line- edge roughness due to stable edge atom configuration.














