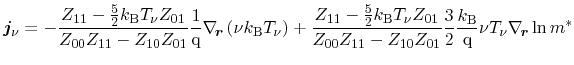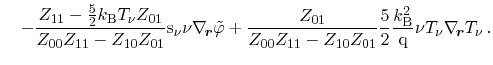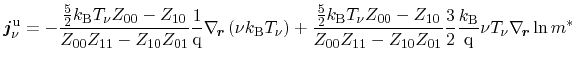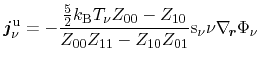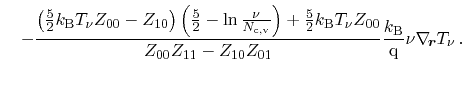3.5.7 Non-Diagonal Relaxation Time Ansatz
In the sequel, an alternative ansatz for the scattering operator is introduced.
Instead of the commonly used relaxation time approximation, the stochastic part
of the moments is modeled using an expansion of the scattering integrals into
the odd moments of the distribution function [90,91].
Thus, the scattering integrals are represented as linear combinations of the
fluxes derived. The weight set chosen for this ansatz is the same as in
Bløtekjær's approach, so the left side of the Boltzmann transport equation can be expressed similarly.
Using the deterministic parts of the particle and energy flux equations from
Eqs. (3.86) and (3.96)
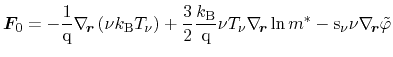 |
|
|
(3.98) |
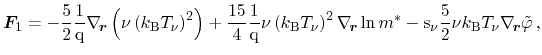 |
|
|
(3.99) |
the corresponding equations are formally expanded as
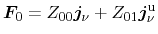 |
|
|
(3.100) |
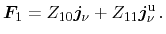 |
|
|
(3.101) |
Since the actual quantities of interest are the particle current
 and the
energy flux density
and the
energy flux density
 , the coupled equations are formulated in order to
explicitly express the particle and energy flux, respectively
, the coupled equations are formulated in order to
explicitly express the particle and energy flux, respectively
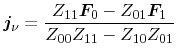 |
|
|
(3.102) |
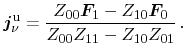 |
|
|
(3.103) |
The fluxes
 and
and
 Eqs. (3.98) and (3.99) are inserted to (3.102) and
thus the particle current equation reads
Eqs. (3.98) and (3.99) are inserted to (3.102) and
thus the particle current equation reads
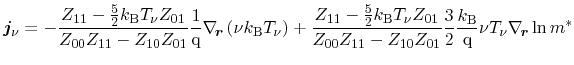 |
|
|
(3.104) |
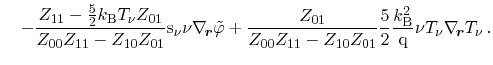 |
|
|
|
Introducing the electrochemical potential (3.62), the current can be
expressed as a linear combination of a
 and a
and a
 expression
expression
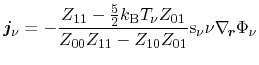 |
|
|
(3.105) |
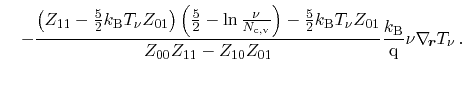 |
|
|
|
For the according energy flux equation, which is expressed analogously, the
fluxes
 and
and
 Eqs. (3.98) and (3.99) are inserted to (3.103)
Eqs. (3.98) and (3.99) are inserted to (3.103)
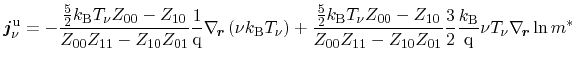 |
|
|
(3.106) |
 |
|
|
|
With the electrochemical potential, it can be rewritten as
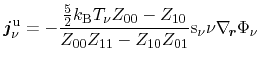 |
|
|
(3.107) |
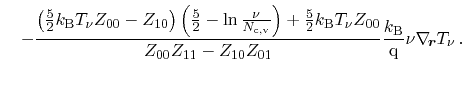 |
|
|
|
A coefficient comparison between the particle flux equation (3.105)
and the according equation derived using Bløtekjær's concept of macroscopic
relaxation times (3.88) enables the identification of several transport
parameters
Analogously to the extended ansatz for the stochastic part of Boltzmann's
equation, these transport coefficients can be seen as an extension to the ones
derived using Bløtekjær's ansatz. Assuming the cross coefficients
 and
and
 to be zero, the coefficients for Bløtekjær's approach carried out in
Section 3.5.6 are obtained. Although the scattering parameters
to be zero, the coefficients for Bløtekjær's approach carried out in
Section 3.5.6 are obtained. Although the scattering parameters
 can
be calculated using accurate physical models, this approach results in a very
complicated description.
can
be calculated using accurate physical models, this approach results in a very
complicated description.
M. Wagner: Simulation of Thermoelectric Devices