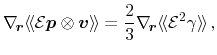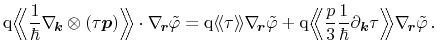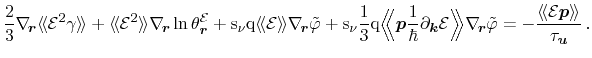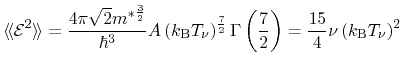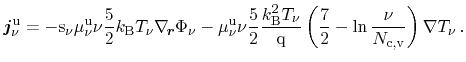3.5.6.2 Energy Flux Equation

With the weight $\ensuremath{\ensuremath{\mathitbf{X}}}= \ensuremath{\mathcal{E}}\ensuremath{\ensuremath{\mathitbf{p}}}$ , one obtains the energy flux equation

$$\underbrace{\vphantom{\frac{1}{\hbar}} \ensuremath{\ensuremath{\e... ...le \! \rangle}}{\ensuremath{{\tau_\ensuremath{\ensuremath{\mathitbf{u}}}}}} \,.$$ (3.89)

The first part is straight-forward

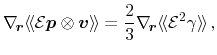$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\en... ... \langle \ensuremath{\mathcal{E}}^2 \ensuremath{\gamma} \rangle \! \rangle} \,,$$ (3.90)

while part (ii) has to be expanded using (A.10). The Poisson bracket $\ensuremath{\{\ensuremath{\mathcal{E}},\ensuremath{\mathcal{E}}\}}$ vanishes because of (A.8) as well as the $\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}\ensuremath{\otimes}}\ensuremath{\ensuremath{\mathitbf{p}}}$ - term. Thus, the second part becomes

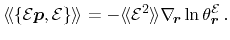$$\ensuremath{\langle \! \langle \ensuremath{\{\ensuremath{\mathcal... ...math{\theta_\ensuremath{\ensuremath{\mathitbf{r}}}^\ensuremath{\mathcal{E}}}\,.$$ (3.91)

The derivative in part (iii) has to be expanded using identity (B.6)

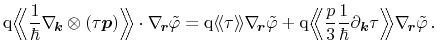$$\mathrm{q}\ensuremath{\Bigl\langle \! \! \Bigl\langle \ensuremath... ...suremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}} \ensuremath{\tilde{\varphi}}\,.$$ (3.92)

Thus, the equation becomes

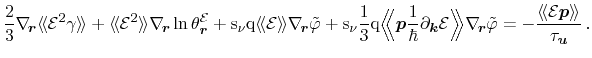$$\frac{2}{3} \ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_... ...le \! \rangle}}{\ensuremath{{\tau_\ensuremath{\ensuremath{\mathitbf{u}}}}}} \,.$$ (3.93)

For parabolic bands and a heated, displaced Maxwellian, the average $\ensuremath{\langle \! \langle \ensuremath{\mathcal{E}}^2 \rangle \! \rangle}$ becomes

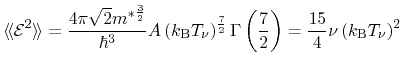$$\ensuremath{\langle \! \langle \ensuremath{\mathcal{E}}^2 \rangle... ...th{\nu}\left( k_\ensuremath{\mathrm{B}}\ensuremath{T_\ensuremath{\nu}}\right)^2$$ (3.94)

analogously to (3.53). While the parts (i) and (ii) are straight-forward to handle, the derivative in part (iii) has to be explicitly expressed which finally also leads to the energy average. Finally, the mobility definition (3.85) already used in the particle flux equation is inserted

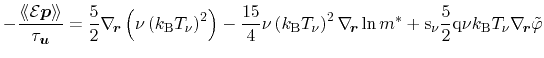$$- \frac{\ensuremath{\langle \! \langle \ensuremath{\mathcal{E}}\e... ...{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{\tilde{\varphi}}$$ (3.95)

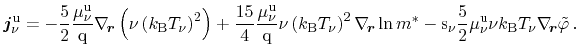$$\ensuremath{\ensuremath{\mathitbf{j}}_\nu^\mathrm{u}}= - \frac{5}... ...nsuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{\tilde{\varphi}}\,.$$ (3.96)

Introducing the electrochemical potential defined in Eqs. (3.60) and (3.62), the energy flux equation becomes

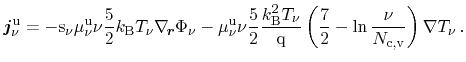$$\ensuremath{\ensuremath{\mathitbf{j}}_\nu^\mathrm{u}}= - \ensurem... ...\ensuremath{\ensuremath{\mathitbf{\nabla}}}} \ensuremath{T_\ensuremath{\nu}}\,.$$ (3.97)

M. Wagner: Simulation of Thermoelectric Devices