3.3.2 Strain due to Vacancy Generation/Annihilation

The generation or annihilation of vacancies is accompanied by a change in the concentration of lattice sites, so that $\Delta\CV = \Delta\CL$ [139]. Thus, the relative volume change of a given test volume due to the addition or removal of lattice sites through a change in the local vacancy concentration $\Delta\CV$ by means of generation/annihilation processes is [147]

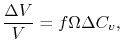$$\frac{\Delta V}{V} = \symVacRelFactor\symAtomVol\Delta\CV,$$ (3.36)

where $\symVacRelFactor\symAtomVol$ accounts for the vacancy volume. Following the same procedure as described above, the strain rate is given by

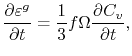$$\ensuremath{\ensuremath{\frac{\partial \symStrain^g}{\partial t}}... ...cRelFactor\symAtomVol\ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}},$$ (3.37)

where $\symStrain^g$ refers to the strain produced due to vacancy generation/annihilation processes.

Since the change in vacancy concentration is given by generation or annihilation processes

$$\ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}} = \G,$$ (3.38)

which leads to the generation/annihilation strain rate components

$$\ensuremath{\ensuremath{\frac{\partial \symVacGenStrain}{\partial t}}} = \left[\frac{1}{3}\symVacRelFactor\symAtomVol\G\right]\symKronecker.$$ (3.39)