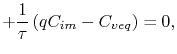Next: 4.2.4 Discretization of the
Up: 4.2 Discretization of the
Previous: 4.2.2 Discretization of the
4.2.3 Discretization of the Vacancy Balance Equation
The combination of (3.74) with (3.75) and (3.76) yields the vacancy balance equation
| |
![$\displaystyle \ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}} +\ensur...
...Factor\symAtomVol}{\kB\T}\CV\ensuremath{\nabla{\symHydStress}}\biggr) \right]}}$](img527.png) |
|
| |
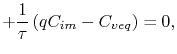 |
(4.41) |
for which the weak formulation of the form
is obtained under the assumption of a Neumann boundary condition.
Applying the electric potential and the temperature discretization, (4.29) and (4.36), respectively,
together with
 |
(4.43) |
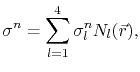 |
(4.44) |
 |
(4.45) |
and the backward Euler time discretization, the vacancy balance equation discretized in a single element is given by
under the assumption that
 ,
,  , and
, and  are constant inside an element.
are constant inside an element.
Using the shorthand notation (4.31), (4.38), (4.39), and
 |
(4.47) |
(4.46) is written as
In the above derivation the vacancy diffusivity is treated as a scalar diffusion coefficient. In order to take into account the anisotropy of diffusivity due to the mechanical stress, as presented in Section 3.2.2, a diffusivity tensor must be applied. This requires a slight modification of (4.48) to
where the diffusivity tensor
 is now incorporated into
is now incorporated into  and
and
 , given by
, given by
 |
(4.50) |
and
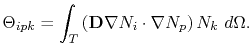 |
(4.51) |
At material interfaces and grain boundaries the trapped vacancy concentration is governed by (3.76), rewritten here as
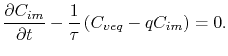 |
(4.52) |
The finite element formulation of this equation follows the same procedure described above, which yields the discretization
| |
 |
|
| |
 |
(4.53) |




Next: 4.2.4 Discretization of the
Up: 4.2 Discretization of the
Previous: 4.2.2 Discretization of the
R. L. de Orio: Electromigration Modeling and Simulation
![$\displaystyle \ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}} +\ensur...
...Factor\symAtomVol}{\kB\T}\CV\ensuremath{\nabla{\symHydStress}}\biggr) \right]}}$](img527.png)