



Next: 4.3 Simulation in FEDOS
Up: 4.2 Discretization of the
Previous: 4.2.3 Discretization of the
4.2.4 Discretization of the Mechanical Equations
The deformation in a three-dimensional body is expressed by the displacement field
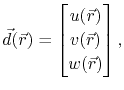 |
(4.54) |
where  ,
,  , and
, and  are the displacements in the x, y, and z direction, respectively.
The displacement is discretized on a tetrahedral element as [151]
are the displacements in the x, y, and z direction, respectively.
The displacement is discretized on a tetrahedral element as [151]
 |
(4.55) |
which leads to the components discretization
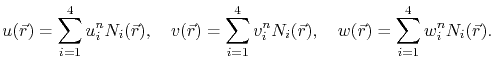 |
(4.56) |
Applying this discretization in the strain-displacement relationship (3.79), the components of the strain tensor can be written as
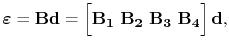 |
(4.57) |
where
 is the matrix of the derivatives of the shape functions for the node i [151]
is the matrix of the derivatives of the shape functions for the node i [151]
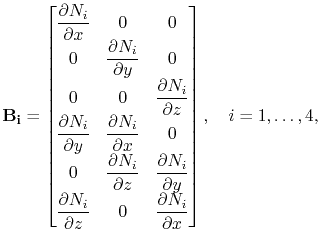 |
(4.58) |
and the displacement matrix
 |
(4.59) |
Using (4.57), the stress-strain equation (3.81) can written as a function of the displacements according to
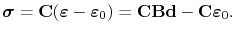 |
(4.60) |
Applying the principle of virtual work, the work of internal stresses on a continuous elastic body is given by [151]
 |
(4.61) |
where
 is the transposed strain tensor.
Combining (4.57), (4.60), and (4.61) the work on a finite element is written as
is the transposed strain tensor.
Combining (4.57), (4.60), and (4.61) the work on a finite element is written as
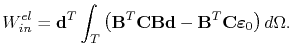 |
(4.62) |
From energy balance the internal work should be equal to the work done by external forces, i.e.
 , and, since during electromigration there are no external forces (
, and, since during electromigration there are no external forces ( ), one obtains
), one obtains
 |
(4.63) |
or
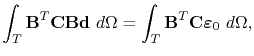 |
(4.64) |
which can be conveniently expressed as
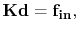 |
(4.65) |
where
 |
(4.66) |
is the so-called stiffness matrix, and
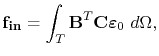 |
(4.67) |
is the internal force vector.
Equation (4.65) forms a linear system of equations of 12 equations with 12 unknowns (the three displacement components  ,
,  , and
, and  for each tetrahedron node).
The inelastic strain
for each tetrahedron node).
The inelastic strain
 determines the internal force vector according to the electromigration induced strain given by (3.78).
determines the internal force vector according to the electromigration induced strain given by (3.78).




Next: 4.3 Simulation in FEDOS
Up: 4.2 Discretization of the
Previous: 4.2.3 Discretization of the
R. L. de Orio: Electromigration Modeling and Simulation
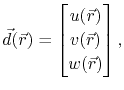
![]() ,
, ![]() , and
, and ![]() for each tetrahedron node).
The inelastic strain
for each tetrahedron node).
The inelastic strain
![]() determines the internal force vector according to the electromigration induced strain given by (3.78).
determines the internal force vector according to the electromigration induced strain given by (3.78).