3.1.5 The Insulator Equations

In insulating materials only the Poisson equation (3.1) and the lattice heat flow equation (3.14) are solved. The presence of doping and mobile carriers is neglected ($n=p=C=0$), therefore the carrier continuity equations are not solved. This assumption leads to the reduction of (3.1) to the Laplace equation (3.18) and the neglecting of the heat generation term of (3.14), which is invoked for semiconductor segments only.

$$\mathrm{div}(\varepsilon_{\mathrm{}} \cdot\mathrm{grad} \psi) = 0$$ (3.18)

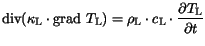$$\mathrm{div}(\kappa_{\mathrm{L}}\cdot\mathrm{grad} T_{{\mathrm{L... ...athrm{L}}\cdot c_{\mathrm{L}}\cdot \frac{\partial T_{{\mathrm{L}}}}{\partial t}$$ (3.19)

Thus, as a result no currents flow through insulators and the influence of the charges inside the insulators is neglected. This assumptions can be neglected, in case of the insulator is treated as a semiconductor material. This approach was successfully applied to Si$_3$N$_4$ and shall be illustrated later in this work. Another approach is the consideration of charges at the semiconductor/insulator interface, which is discussed in the next subsection.