



Next: 3.6.2 The Relaxation Time
Up: 3.6 Energy Relaxation Time
Previous: 3.6 Energy Relaxation Time
Subsections
Depending on the semiconductor material under investigation, different results
are available from Monte-Carlo simulation. Two methods - direct and
indirect - are used to obtain
 .
.
For Si, Ge and GaAs, the dependence of the electron energy relaxation time and
the average electron energy,  , on the electric field are available in
[94]. The average energy is approximated by the thermal energy, with
the kinetic term being neglected:
, on the electric field are available in
[94]. The average energy is approximated by the thermal energy, with
the kinetic term being neglected:
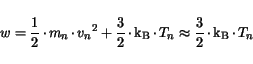 |
(3.136) |
where  ,
,  , and
, and  are the electron mass, velocity and temperature,
respectively. This approximation, together with the interpolation of the
Monte-Carlo simulation results for different electric fields allows to obtain
directly
are the electron mass, velocity and temperature,
respectively. This approximation, together with the interpolation of the
Monte-Carlo simulation results for different electric fields allows to obtain
directly
 as a function of the electron temperature at different
lattice temperatures. This procedure is called direct method.
as a function of the electron temperature at different
lattice temperatures. This procedure is called direct method.
In the case of binary and ternary III-V compounds, such as InAs, AlAs,
In Ga
Ga As, and Al
As, and Al Ga
Ga As, the dependence of
As, the dependence of
 on the
electric field is not available. In this case
on the
electric field is not available. In this case
 is calculated in an
indirect way, using the dependence of the electron velocity on the electric
field from [94]. The local energy balance equation [86] is
obtained by neglecting the energy flux:
is calculated in an
indirect way, using the dependence of the electron velocity on the electric
field from [94]. The local energy balance equation [86] is
obtained by neglecting the energy flux:
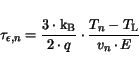 |
(3.137) |
where  is the electron charge,
is the electron charge,
 the lattice temperature, and
the lattice temperature, and  is
the electric field. Using (3.136) and the dependences of the average
electron energy and the electron velocity on the electric field,
is
the electric field. Using (3.136) and the dependences of the average
electron energy and the electron velocity on the electric field,
 is
extracted. This procedure is called indirect method.
is
extracted. This procedure is called indirect method.
Fig. 3.39 shows
 for GaAs as a function of the electron
temperature at
for GaAs as a function of the electron
temperature at
 =300 K, as it results from both the direct and indirect
methods. The correct values are extracted by the direct method as it is based
on less approximations. It turns out that
=300 K, as it results from both the direct and indirect
methods. The correct values are extracted by the direct method as it is based
on less approximations. It turns out that
 is overestimated by using
(3.137) in the indirect method. Nevertheless, the saturation
value of
is overestimated by using
(3.137) in the indirect method. Nevertheless, the saturation
value of
 at high electron temperatures,
at high electron temperatures,
 ,
and the location of the peak,
,
and the location of the peak,
 , are independent of the
methodology used. This criteria are used for correct estimation of
, are independent of the
methodology used. This criteria are used for correct estimation of
 in materials where only the indirect method can be applied.
in materials where only the indirect method can be applied.
Figure 3.39:
Energy relaxation time as a function of electron temperature:
Results from the direct and indirect method for GaAs
|
|




Next: 3.6.2 The Relaxation Time
Up: 3.6 Energy Relaxation Time
Previous: 3.6 Energy Relaxation Time
Vassil Palankovski
2001-02-28
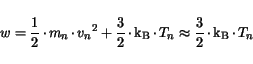
![]() for GaAs as a function of the electron
temperature at
for GaAs as a function of the electron
temperature at
![]() =300 K, as it results from both the direct and indirect
methods. The correct values are extracted by the direct method as it is based
on less approximations. It turns out that
=300 K, as it results from both the direct and indirect
methods. The correct values are extracted by the direct method as it is based
on less approximations. It turns out that
![]() is overestimated by using
(3.137) in the indirect method. Nevertheless, the saturation
value of
is overestimated by using
(3.137) in the indirect method. Nevertheless, the saturation
value of
![]() at high electron temperatures,
at high electron temperatures,
![]() ,
and the location of the peak,
,
and the location of the peak,
![]() , are independent of the
methodology used. This criteria are used for correct estimation of
, are independent of the
methodology used. This criteria are used for correct estimation of
![]() in materials where only the indirect method can be applied.
in materials where only the indirect method can be applied.
![\resizebox{\halflength}{!}{
\includegraphics[width=\halflength]{figs/Ctwdi.eps}}](img629.gif)