



Next: 3.7.2 Auger Recombination
Up: 3.7 Generation and Recombination
Previous: 3.7 Generation and Recombination
3.7.1 Shockley-Read-Hall and Surface Recombination
Carrier generation in space charge regions and recombination in e.g. high
injection regions is modeled using the well known Shockley-Read-Hall
(SRH)
equation
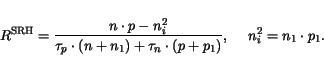 |
(3.142) |
The auxiliary variables  and
and  are defined by
are defined by
For trap energy level
 located in the mid gap
located in the mid gap  and the
recombination rate has its maximum. The variables
and the
recombination rate has its maximum. The variables  and
and  are the
carrier effective densities of states (see
Section 3.3). The dependence on the lattice temperature
are the
carrier effective densities of states (see
Section 3.3). The dependence on the lattice temperature
 is given by the variables
is given by the variables
 and
and
 and the
recombination lifetimes for electrons and holes,
and the
recombination lifetimes for electrons and holes,
 and
and
 . The thermal carrier velocities at 300 K are calculated
using
. The thermal carrier velocities at 300 K are calculated
using
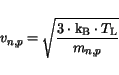 |
(3.145) |
to obtain the recombination times at 300 K
The recombination times are modeled using traps of donor, acceptor, or neutral
type, respectively, of trap density
 , and the trap capture cross sections
for electrons and holes,
, and the trap capture cross sections
for electrons and holes,
 and
and
 .
The effect of surface recombination is included by using non-zero surface
recombination velocities for electrons
.
The effect of surface recombination is included by using non-zero surface
recombination velocities for electrons  and holes
and holes  , respectively.
The effect is stronger with decreasing distance to the surface
, respectively.
The effect is stronger with decreasing distance to the surface  .
.
Finally, the temperature dependence is included. The effect of trap assisted
band to band tunneling (TBB) in Si is accounted for by a field enhancement
factors  and
and  , which are modeled after [187].
As TBB is of importance only for materials with indirect bandgap this effect is
neglected in literature for technologically important III-V materials, which
have a direct bandgap (see Section 3.3.1).
, which are modeled after [187].
As TBB is of importance only for materials with indirect bandgap this effect is
neglected in literature for technologically important III-V materials, which
have a direct bandgap (see Section 3.3.1).
The default values recommended for the SRH recombination model are summarized in the
following table:
Table 3.35:
Parameter values for SRH recombination model
| Material |
 [cm [cm ] ] |
 [eV] [eV] |
 [m [m ] ] |
 [m [m ] ] |
 [m/s] [m/s] |
 [m/s] [m/s] |
| Si, Ge |
1e13 |
0.0 |
1e-15 |
1e-15 |
0.0 |
0.0 |
| III-Vs |
2e16 |
0.4 |
1e-14 |
1e-13 |
0.0 |
0.0 |
|




Next: 3.7.2 Auger Recombination
Up: 3.7 Generation and Recombination
Previous: 3.7 Generation and Recombination
Vassil Palankovski
2001-02-28
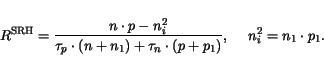
![]() and
and ![]() are defined by
are defined by
![]() and
and ![]() , which are modeled after [187].
As TBB is of importance only for materials with indirect bandgap this effect is
neglected in literature for technologically important III-V materials, which
have a direct bandgap (see Section 3.3.1).
, which are modeled after [187].
As TBB is of importance only for materials with indirect bandgap this effect is
neglected in literature for technologically important III-V materials, which
have a direct bandgap (see Section 3.3.1).