



Next: 3.3.2 Bandgap Offsets
Up: 3.3 Band-Structure
Previous: 3.3 Band-Structure
Subsections
3.3.1 Bandgap Energy
The bandgap (or forbidden energy zone) is one of the most important
semiconductor parameters. Various models define the temperature dependence of
the bandgap energy in semiconductors (e.g. [112]). For an alloy
 , the temperature-dependent bandgaps of the constituents
(A and B) are calculated first. The bandgap and the energy offset are then
calculated depending on the material composition. This is important to assure
consistency between the values for alloy materials at
, the temperature-dependent bandgaps of the constituents
(A and B) are calculated first. The bandgap and the energy offset are then
calculated depending on the material composition. This is important to assure
consistency between the values for alloy materials at  and
and  and the values
for the respective basic materials. For materials where the bandgap changes between
direct and indirect the multiple valley conduction bands are considered.
and the values
for the respective basic materials. For materials where the bandgap changes between
direct and indirect the multiple valley conduction bands are considered.
In MINIMOS-NT the model of Varshni [112] is used for basic materials. The
temperature dependence is calculated by (3.60), where
 is the bandgap at 0 K.
is the bandgap at 0 K.
| |
|
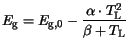 |
(3.60) |
The parameter values are summarized in Table 3.8. Note, for these
materials always the lowest conduction band valley minimum is taken into
account. In addition, the resulting bandgaps at 300 K,
 , are
included in Table 3.9.
, are
included in Table 3.9.
Table 3.8:
Parameter values for modeling the bandgap energies
| Material |
Minimum |
 [eV] [eV] |
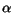 [eV/K] [eV/K] |
 [K] [K] |
Reported
 [eV] [eV] |
References |
| Si |
X |
1.1695 |
4.73
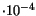 |
636 |
1.17 |
[90,86] |
| Ge |
L |
0.7437 |
4.774
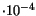 |
235 |
0.74 |
[86] |
| GaAs |
G |
1.521 |
5.58
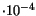 |
220 |
1.51-1.55 |
[113,114,115] |
| AlAs |
X |
2.239 |
6.0
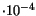 |
408 |
2.22-2.239 |
[94,90,108] |
| InAs |
G |
0.420 |
2.5
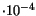 |
75 |
0.414-0.43 |
[92,113] |
| InP |
G |
1.421 |
3.63
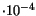 |
162 |
1.42-1.432 |
[108,86,114] |
| GaP |
X |
2.338 |
5.771
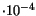 |
372 |
2.338-2.346 |
[108,86,90] |
|
Table 3.9:
Bandgap energies at room temperature compared to reported data
| Material |
Minimum |
 [eV] [eV] |
Reported
 [eV] [eV] |
References |
| Si |
X |
1.124 |
1.12-1.1242 |
[85,86,90] |
| Ge |
L |
0.663 |
0.66-0.67 |
[90,85,86] |
| GaAs |
G |
1.424 |
1.42-1.43 |
[116,95,104,85] |
| AlAs |
X |
2.163 |
2.14-2.168 |
[94,116,104,90] |
| InAs |
G |
0.360 |
0.354-0.37 |
[93,92,115,117] |
| InP |
G |
1.350 |
1.34-1.351 |
[90,115,92] |
| GaP |
X |
2.261 |
2.26-2.272 |
[85,92,90] |
|
For  two additional models can be chosen which are based on
polynomial fits of second and third order. The first one after
Gaensslen [118,119]
was also used in MINIMOS 6. The second model is based on data from
Green [120].
two additional models can be chosen which are based on
polynomial fits of second and third order. The first one after
Gaensslen [118,119]
was also used in MINIMOS 6. The second model is based on data from
Green [120].
| |
|
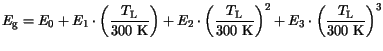 |
(3.61) |
The parameter values for these models are summarized in Table 3.10.
Table 3.10:
Parameter values for modeling the bandgap energies
| Model |
 [eV] [eV] |
 [eV] [eV] |
 [eV] [eV] |
 [eV] [eV] |
 [eV] [eV] |
| Gaensslen |
1.1785 |
-0.02708 |
-0.02745 |
0.0 |
1.124 |
| Green |
1.17 |
0.00572 |
-0.06948 |
0.018 |
1.124 |
|
In Fig. 3.8 the results obtained with the three different models
for Si are compared to data from [120]. In Fig. 3.9 and Fig. 3.10 the
temperature dependence of the direct gap in GaAs and InP, respectively, are
compared to other models.
In the case of alloy materials the temperature-dependent bandgaps of the constituents,
 and
and
 , are calculated by (3.60).
However, for materials where the bandgap changes between direct and indirect
the multiple valley conduction bands are considered. For that purpose,
additional model parameters are needed for the higher energy valleys in the
respective III-V binary materials (Table 3.11). In addition, the
resulting bandgaps at 300 K,
, are calculated by (3.60).
However, for materials where the bandgap changes between direct and indirect
the multiple valley conduction bands are considered. For that purpose,
additional model parameters are needed for the higher energy valleys in the
respective III-V binary materials (Table 3.11). In addition, the
resulting bandgaps at 300 K,
 , are included in Table 3.12.
, are included in Table 3.12.
Table 3.11:
Parameter values for modeling the bandgap energies
| Material |
Minimum |
 [eV] [eV] |
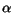 [eV/K] [eV/K] |
 [K] [K] |
Reported
 [eV] [eV] |
References |
| GaAs |
X |
1.981 |
4.6
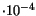 |
204 |
1.9-1.91 |
[116,104] |
| AlAs |
G |
2.891 |
8.78
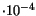 |
332 |
2.907-3.02 |
[59,95,94,104] |
| InAs |
X |
2.278 |
5.78
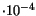 |
83 |
|
|
| InP |
X |
2.32 |
7.66
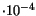 |
327 |
2.32-2.38 |
[109,84,121] |
| GaP |
G |
2.88 |
8.0
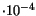 |
300 |
2.869-2.895 |
[91,84,122] |
|
Table 3.12:
Bandgap energies at room temperature compared to reported data
| Material |
Minimum |
 [eV] [eV] |
Reported
 [eV] [eV] |
References |
| GaAs |
X |
1.899 |
1.9-1.91 |
[116,104] |
| AlAs |
G |
2.766 |
2.671-2.766 |
[93,59] |
| InAs |
X |
2.142 |
1.37-2.14 |
[116,108,123] |
| InP |
X |
2.21 |
2.21-2.30 |
[116,123,121] |
| GaP |
G |
2.76 |
2.73-2.85 |
[84] |
|
The bandgap and the energy offset of an alloy
 are calculated by
are calculated by
The bowing parameters
 and
and
 are summarized in
Table 3.13. Additional bowing parameters
are summarized in
Table 3.13. Additional bowing parameters  are given as a reference
for the case when a one-valley bandgap fit is used.
are given as a reference
for the case when a one-valley bandgap fit is used.
Table 3.13:
Parameter values for the bandgap of alloy materials
| Material |
 [eV] [eV] |
 [eV] [eV] |
 [eV] [eV] |
Reported |
References |
| SiGe |
|
|
-0.4 |
-0.4 |
[124] |
| AlGaAs |
0.0 |
-0.143 |
0.7 |
0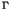 , -0.143 , -0.143 |
[93,125] |
| InGaAs |
|
|
-0.475 |
-0.4, -0.475, -0.555 |
[108,90,71] |
| InAlAs |
-0.3 |
-0.713 |
1.2 |
-0.689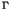 ,-0.24 ,-0.24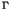 |
[108,90] |
| InAsP |
|
|
-0.32 |
-0.101, -0.32 |
[108,90] |
| GaAsP |
-0.21 |
-0.21 |
0.5 |
-0.176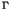 ,-0.23 ,-0.23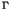 |
[108,126] |
| InGaP |
-0.67 |
-0.17 |
0.6 |
-0.786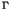 ,-0.6 ,-0.6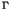 ,-0.18 ,-0.18 |
[108,90,109] |
|
For example, such a one-valley bandgap fit is used in the case of the
technologically important strained Si Ge
Ge grown on Si (see
Fig. 3.11). In certain cases for
grown on Si (see
Fig. 3.11). In certain cases for  the bandgap can become smaller than the
one of pure Ge [127] depending on the strain. In the unstrained case,
however, an
the bandgap can become smaller than the
one of pure Ge [127] depending on the strain. In the unstrained case,
however, an  -to-
-to- gap transition is observed at about
gap transition is observed at about  .
.
The material composition dependence of the  ,
,  , and
, and  -band
gaps in Al
-band
gaps in Al Ga
Ga As at 300 K is shown in Fig. 3.12. A
direct-to-indirect gap transition is observed at about
As at 300 K is shown in Fig. 3.12. A
direct-to-indirect gap transition is observed at about  . The one-valley
bandgap fit which is included for comparison gives a good agreement only for
. The one-valley
bandgap fit which is included for comparison gives a good agreement only for
 . In Fig. 3.13 the temperature dependence of the bandgap in
Al
. In Fig. 3.13 the temperature dependence of the bandgap in
Al Ga
Ga As with Al content as a parameter is shown. In Fig. 3.14
the material composition dependence of the
As with Al content as a parameter is shown. In Fig. 3.14
the material composition dependence of the  ,
,  , and
, and  -band
gaps in In
-band
gaps in In Ga
Ga As at 300 K is shown. As can be seen this material has
a direct bandgap for the entire composition range. Therefore, only the energy
of the
As at 300 K is shown. As can be seen this material has
a direct bandgap for the entire composition range. Therefore, only the energy
of the  valley is taken into account. However, in the case of strain
the bandgap can significantly differ [128]. For example, a good fit to
the strained bandgap values of In
valley is taken into account. However, in the case of strain
the bandgap can significantly differ [128]. For example, a good fit to
the strained bandgap values of In Ga
Ga As grown on GaAs can be achieved
by changing the
As grown on GaAs can be achieved
by changing the
 of InAs from 0.42 eV to 0.58 eV. In Fig. 3.15 the
temperature dependence of the bandgap in In
of InAs from 0.42 eV to 0.58 eV. In Fig. 3.15 the
temperature dependence of the bandgap in In Ga
Ga As with In content as
a parameter is shown. In the case of In
As with In content as
a parameter is shown. In the case of In Al
Al As there is
direct-to-indirect gap transition at about
As there is
direct-to-indirect gap transition at about  and the use of one valley
fit is nearly impossible. It gives comparatively accurate values for the
lattice matched case of
and the use of one valley
fit is nearly impossible. It gives comparatively accurate values for the
lattice matched case of  and above (see Fig. 3.16).
InAs
and above (see Fig. 3.16).
InAs P
P has a direct gap for the complete material composition range
so only the
has a direct gap for the complete material composition range
so only the  valley energy is calculated. The bowing parameter value
suggested in [108] is used. GaAs
valley energy is calculated. The bowing parameter value
suggested in [108] is used. GaAs P
P has a direct-to-indirect
gap transition at about
has a direct-to-indirect
gap transition at about  . As can be seen in Fig. 3.17 a one valley
model can be successfully used for this material. In Fig. 3.18 the
material composition dependence of the
. As can be seen in Fig. 3.17 a one valley
model can be successfully used for this material. In Fig. 3.18 the
material composition dependence of the  ,
,  , and
, and  -bandgaps
in Ga
-bandgaps
in Ga In
In P at 300 K is shown. The direct-to-indirect gap transition
is at about
P at 300 K is shown. The direct-to-indirect gap transition
is at about  . Only at the technologically important value of
. Only at the technologically important value of  ,
when Ga
,
when Ga In
In P lattice matches the one of GaAs the one-valley model
gives a good fit for the bandgap. The temperature dependence of the bandgap in
Ga
P lattice matches the one of GaAs the one-valley model
gives a good fit for the bandgap. The temperature dependence of the bandgap in
Ga In
In P with Ga content as a parameter is shown in Fig. 3.19.
P with Ga content as a parameter is shown in Fig. 3.19.
Figure 3.8:
Comparison of different models for the
temperature dependence of the bandgap in Si
|
|
Figure 3.9:
Comparison of different models for the
temperature dependence of the bandgap in GaAs
|
|
Figure 3.10:
Comparison of different models for the
temperature dependence of the bandgap in InP
|
|
Figure 3.11:
Material composition dependence of the
 ,
,  , and
, and  -bandgaps in Si
-bandgaps in Si Ge
Ge at 300 K
at 300 K
|
|
Figure 3.12:
Material composition dependence of the
 ,
,  , and
, and  -bandgaps in Al
-bandgaps in Al Ga
Ga As at 300 K
As at 300 K
|
|
Figure 3.13:
Temperature dependence of the bandgap
in Al Ga
Ga As with Al content as a parameter
As with Al content as a parameter
|
|
Figure 3.14:
Material composition dependence of the
 ,
,  , and
, and  -bandgaps in In
-bandgaps in In Ga
Ga As at 300 K
As at 300 K
|
|
Figure 3.15:
Temperature dependence of the bandgap
in In Ga
Ga As with In content as a parameter
As with In content as a parameter
|
|
Figure 3.16:
Material composition dependence of the
 ,
,  , and
, and  -bandgaps in In
-bandgaps in In Al
Al As at 300 K
As at 300 K
|
|
Figure 3.17:
Material composition dependence of the
 ,
,  , and
, and  -bandgaps in GaAs
-bandgaps in GaAs P
P at 300 K
at 300 K
|
|
Figure 3.18:
Material composition dependence of the
 ,
,  , and
, and  -bandgaps in Ga
-bandgaps in Ga In
In P at 300 K
P at 300 K
|
|
Figure 3.19:
Temperature dependence of the bandgap
in Ga In
In P with Ga content as a parameter
P with Ga content as a parameter
|
|




Next: 3.3.2 Bandgap Offsets
Up: 3.3 Band-Structure
Previous: 3.3 Band-Structure
Vassil Palankovski
2001-02-28
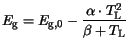
![]() two additional models can be chosen which are based on
polynomial fits of second and third order. The first one after
Gaensslen [118,119]
was also used in MINIMOS 6. The second model is based on data from
Green [120].
two additional models can be chosen which are based on
polynomial fits of second and third order. The first one after
Gaensslen [118,119]
was also used in MINIMOS 6. The second model is based on data from
Green [120].
![]() are calculated by
are calculated by
![]() ,
, ![]() , and
, and ![]() -band
gaps in Al
-band
gaps in Al![]() Ga
Ga![]() As at 300 K is shown in Fig. 3.12. A
direct-to-indirect gap transition is observed at about
As at 300 K is shown in Fig. 3.12. A
direct-to-indirect gap transition is observed at about ![]() . The one-valley
bandgap fit which is included for comparison gives a good agreement only for
. The one-valley
bandgap fit which is included for comparison gives a good agreement only for
![]() . In Fig. 3.13 the temperature dependence of the bandgap in
Al
. In Fig. 3.13 the temperature dependence of the bandgap in
Al![]() Ga
Ga![]() As with Al content as a parameter is shown. In Fig. 3.14
the material composition dependence of the
As with Al content as a parameter is shown. In Fig. 3.14
the material composition dependence of the ![]() ,
, ![]() , and
, and ![]() -band
gaps in In
-band
gaps in In![]() Ga
Ga![]() As at 300 K is shown. As can be seen this material has
a direct bandgap for the entire composition range. Therefore, only the energy
of the
As at 300 K is shown. As can be seen this material has
a direct bandgap for the entire composition range. Therefore, only the energy
of the ![]() valley is taken into account. However, in the case of strain
the bandgap can significantly differ [128]. For example, a good fit to
the strained bandgap values of In
valley is taken into account. However, in the case of strain
the bandgap can significantly differ [128]. For example, a good fit to
the strained bandgap values of In![]() Ga
Ga![]() As grown on GaAs can be achieved
by changing the
As grown on GaAs can be achieved
by changing the
![]() of InAs from 0.42 eV to 0.58 eV. In Fig. 3.15 the
temperature dependence of the bandgap in In
of InAs from 0.42 eV to 0.58 eV. In Fig. 3.15 the
temperature dependence of the bandgap in In![]() Ga
Ga![]() As with In content as
a parameter is shown. In the case of In
As with In content as
a parameter is shown. In the case of In![]() Al
Al![]() As there is
direct-to-indirect gap transition at about
As there is
direct-to-indirect gap transition at about ![]() and the use of one valley
fit is nearly impossible. It gives comparatively accurate values for the
lattice matched case of
and the use of one valley
fit is nearly impossible. It gives comparatively accurate values for the
lattice matched case of ![]() and above (see Fig. 3.16).
InAs
and above (see Fig. 3.16).
InAs![]() P
P![]() has a direct gap for the complete material composition range
so only the
has a direct gap for the complete material composition range
so only the ![]() valley energy is calculated. The bowing parameter value
suggested in [108] is used. GaAs
valley energy is calculated. The bowing parameter value
suggested in [108] is used. GaAs![]() P
P![]() has a direct-to-indirect
gap transition at about
has a direct-to-indirect
gap transition at about ![]() . As can be seen in Fig. 3.17 a one valley
model can be successfully used for this material. In Fig. 3.18 the
material composition dependence of the
. As can be seen in Fig. 3.17 a one valley
model can be successfully used for this material. In Fig. 3.18 the
material composition dependence of the ![]() ,
, ![]() , and
, and ![]() -bandgaps
in Ga
-bandgaps
in Ga![]() In
In![]() P at 300 K is shown. The direct-to-indirect gap transition
is at about
P at 300 K is shown. The direct-to-indirect gap transition
is at about ![]() . Only at the technologically important value of
. Only at the technologically important value of ![]() ,
when Ga
,
when Ga![]() In
In![]() P lattice matches the one of GaAs the one-valley model
gives a good fit for the bandgap. The temperature dependence of the bandgap in
Ga
P lattice matches the one of GaAs the one-valley model
gives a good fit for the bandgap. The temperature dependence of the bandgap in
Ga![]() In
In![]() P with Ga content as a parameter is shown in Fig. 3.19.
P with Ga content as a parameter is shown in Fig. 3.19.