3.3.2 Bandgap Offsets

The problem to align the bandgaps of two or more different materials is old and not completely solved [129,130,131] due to the dependence on the growth conditions. The many suggested approaches mainly differ in whether to use the electron affinity to align the conduction bands, whether to align the midgaps, or whether to align the valence band edges. In MINIMOS-NT the last approach is used.

An energy offset, $E_{\mathrm{off}}$, is used to align the band edge energies of different materials. $E_{\mathrm{off}}$ is an arbitrary value and by changing it consistently for all materials at the same time the same results are obtained. As a default in MINIMOS-NT for the group IV materials the reference material is Si. The origin of the energy axis is assumed to be in the middle of the Si bandgap at 300 K. This corresponds to a fixed value for Si of $E_{\mathrm{off}}=-E_{\mathrm{g}}/2=-0.562$ eV. For the III-V material system GaAs is chosen as the reference material. Therefore, the offset for GaAs is $E_{\mathrm{off}}=-E_{\mathrm{g}}/2=-0.712$ eV. The default offsets for other materials, summarized in Table 3.14, are chosen to give good agreement with reported data from [108,111,129,130,131].

Table 3.14: Parameter values for modeling the bandgap energies

Material	$E_{\mathrm{off}}$ [eV]	Material	$E_{\mathrm{off}}$ [eV]
Si	-0.562	InAs	-0.286
Ge	-0.157	InP	-0.724
GaAs	-0.712	GaP	-1.062
AlAs	-1.008

The energies of the conduction and valence band edges are calculated by

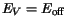$$E_{V}= E_{\mathrm{off}}$$ (3.66)

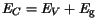$$E_{C}= E_{V}+E_{\mathrm{g}}$$ (3.67)

For alloy materials, the following expressions for the conduction and valence band energies are often used.

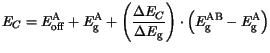$$E_{C}= E_{\mathrm{off}}^\mathrm {A} + E_{\mathrm{g}}^\mathrm {A} ... ...ght)\cdot \left(E_{\mathrm{g}}^\mathrm {AB} - E_{\mathrm{g}}^\mathrm {A}\right)$$ (3.68)

$$E_{V}= E_{C}- E_{\mathrm{g}}^\mathrm {AB}$$ (3.69)

The change of the bandgap with the material composition is defined by the ratio $\Delta E_{C}/\Delta E_{\mathrm{g}}$, starting from one of the materials. For example, for Al$_x$Ga$_{1-x}$As/GaAs interface it is known that this ratio equals 60%. This means that, with increasing $x$, 60% of the increase of the bandgap ( $\Delta E_{\mathrm{g}}= \Delta E_{C}+ \Delta E_{V}$) is contributed to the conduction band ($\Delta E_{C}$) and 40% to the valence band ($\Delta E_{V}$). The model, being so formulated, is not symmetric and general enough. However, assuming $\Delta E_{C}/\Delta E_{\mathrm{g}}$ is constant for the whole composition range one obtains:

$$E_{C} = E_{\mathrm{off}}^\mathrm {B} + E_{\mathrm{g}}^\mathrm {B} + \left... ...ght)\cdot \left(E_{\mathrm{g}}^\mathrm {AB} - E_{\mathrm{g}}^\mathrm {B}\right)$$ (3.70)

Thus, from (3.68) and (3.70) the ratio $\Delta E_{C}/\Delta E_{\mathrm{g}}$ can be expressed as:

$$\Delta E_{C}/\Delta E_{\mathrm{g}} = 1 + \frac{E_{\mathrm{off}}^\mathrm {A} - E_{\mathrm{off}}^\mathrm {B}}{E_{\mathrm{g}}^\mathrm {A} - E_{\mathrm{g}}^\mathrm {B}}$$ (3.71)

Replacing it in (3.68) or (3.70) the offset of alloy material is obtained:

$$E_{\mathrm{off}}^\mathrm {AB} = \frac{E_{\mathrm{off}}^\mathrm {A}\cdot\left(E_{\mathrm{g}}^\math... ...g}}^\mathrm {A}\right)} {E_{\mathrm{g}}^\mathrm {A}-E_{\mathrm{g}}^\mathrm {B}}$$ (3.72)

The valence and the conduction band energies are calculated by (3.66) and (3.67), respectively. Using the default model parameters in MINIMOS-NT ratios $\Delta E_{C}/\Delta E_{\mathrm{g}}$ of 0.12 for SiGe, 0.6 for AlGaAs, 0.5 for InAlAs, 0.6 for InGaAs, InAsP, GaAsP, and 0.3 for InGaP are obtained, which are in fairly good agreement with experimental data [110,89,111,108,132].

The complete bandgap alignment of all semiconductor materials presented in MINIMOS-NT is shown in Fig. 3.20.

Figure 3.20: Bandgaps of all semiconductor materials modeled in MINIMOS-NT: Reference energies for IV group and III-V group materials are the mid gaps of Si and GaAs, respectively, placed at 0 eV.

Special attention is paid to the band offsets at the heterointerfaces and thermionic emission or thermionic-field emission model must be used in the case of abrupt heterojunctions (see Section 3.1.6).