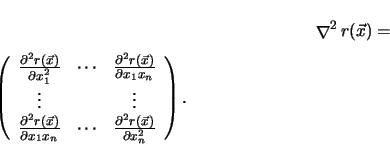4.1.6.1 Hessian Matrix

The Hessian matrix $\mathop{\nabla }\nolimits ^2 r(\vec{x})$ of a scalar function $r(\vec{x})$ ( $\vec{x} \in \mathbb{R}^{n}$) is defined by the n x n matrix built out of the second partial derivatives

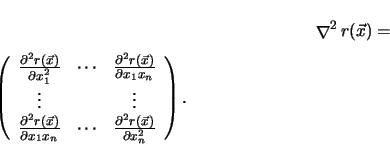$$\mathop{\nabla }\nolimits ^2 r(\vec{x}) = \left ( \beg... ...tial^2 r(\vec{x})}{\partial x_n^2} \\ \end{array} \right ) .$$ (4.19)

The use of a finite-difference approximation of the first derivatives is not suitable for this purpose. They would need a very large amount of function evaluations.

A good approximation of the curvature of the nonlinear function without additional function evaluations can be computed by an iterative scheme, where the gradient of the current and last step and the Hessian of the last step are used.

In the Broyden-Fletcher-Goldfarb-Shanno [63] (BFGS) update the approximative Hessian matrix $\mathcal{B}_{k+1}$^4.2 is calculated from the approximation of the last step $\mathcal{B}_{k}$ with:

$$\mathcal{B}_{k+1} = \mathcal{B}_{k} + \frac{1}{\vec{g}_k^... ...{\vec{y}_k^{\cal T} \vec{s}_k} \vec{y}_k \vec{y}_k^{\cal T} .$$ (4.20)

In (4.20) the vectors $\vec{s}_k = \vec{x}_{k-1} - \vec{x}_k$ denote the last step and $\vec{y}_k = \vec{g}_{k-1} - \vec{g}_k$ the difference of the gradient vectors. The direction of search is assumed to be the Newton direction (see 4.1.4).

The algorithm starts with the identity matrix as an initial value of the approximated Hessian matrix. Hence the first iteration of the Newton step is equivalent to an iteration of a steepest-descent method.

Other iterative update formulas are the Powell-Symmetric-Broyden (PSB)

$$\mathcal{B}_{k+1} = \mathcal{B}_{k} + \frac{1}{\vec{s}_k^{... ...^{\cal T} \vec{s}_k \right ) ^2 } \vec{s}_k \vec{s}_k^{\cal T}$$ (4.21)

and the Davidon-Fletcher-Powell (DFP) update [19]

$$\mathcal{B}_{k+1} = \mathcal{B}_{k} - \frac{1}{\vec{s}_k^... ...athcal{B}_{k} \vec{s}_k \right ) \vec{w}_k \vec{w}_k^{\cal T}$$ (4.22)

with

$$\vec{w}_k = \frac{1}{\vec{y}_k^{\cal T} \vec{s}_k} \vec{y... ...l T} \mathcal{B}_{k} \vec{s}_k} \mathcal{B}_{k} \vec{s}_k .$$ (4.23)

It is now general believe that the most effective update is the BFGS update [19]

Footnotes

... $\mathcal{B}_{k+1}$^4.2

The index of the matrix $\mathcal{B}_{k}$ means the matrix $\mathcal{B}$ of the k iteration.