3.2.2 Direct radiation from plane edges on the PCB

According to [59] the estimation for the maximum radiated electric far field density from rectangular power planes on a PCB as depicted in Figure 3.2 is

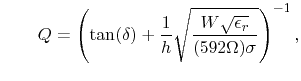$$E_{max}(f)\approx\left(120\Omega\right)\cdot\frac{I_{noise}(f)h}{r\epsilon_{r}W}\cdot Q \qquad Q=\left(\tan(\delta)+\frac{1}{h}\sqrt{\frac{W\sqrt{\epsilon_{r}}}{(592\Omega)\sigma}}\right)^{-1},$$ (3.2)

where s is the conductivity of the planes, r is the distance of the field observation point from the PCB, I_noise(f) is the magnitude of the harmonic at frequency f of the noise current I_noise, e_r is the relative permittivity, and tan(d) is the loss tangent of the PCB substrate. Maximum radiation occurs at the parallel plane resonances

$$f_{r}\approx \frac{c_{0}}{2\pi\sqrt{\epsilon_{r}}}\sqrt{\left(\frac{m\pi}{L}\right)^2+\left(\frac{n\pi}{W}\right)^2},$$ (3.3)

where m and n are positive integer values and c₀ denotes the speed of light in vacuum. Note that this is a good first order estimation, intended to classify the direct radiation of PCB planes regarding their ability to exceed an emission limit. This estimation considers neither the influence of shields on the PCB, nor the influence of an enclosure or the influence of the position of the noise current on the planes. The power plane noise current I_noise has to be obtained from a network simulation which considers the integrated circuits with ICEM models [60], [61] and the power plane impedance. The power plane impedance for rectangular planes is obtained from (4.18) [59]. A powerful finite element method for the impedance simulation of fairly arbitrary shaped planes is described in Section 4.4.

Figure 3.2: Radiating current loop on a PCB.

C. Poschalko: The Simulation of Emission from Printed Circuit Boards under a Metallic Cover