The estimated characteristic parameters of distributions fitted by central
moments are often markedly less accurate than those obtained by other
estimation procedures. We present an alternative approach, where we
introduce the so-called probability weighted moments (PWMs) in
combination with the L-moments to specify statistical
distributions [Hos89]. To our knowledge, we used this approach the
first time in semiconductor simulation engineering. These L-moments
are analogous to conventional central moments, but can be estimated by
linear combinations of order statistics. L-moments are able to
characterize a wider range of distribution functions and are more robust
against outliers in the given data set than central moments. These
L-moments can be defined in terms of probability weighted moments
by a linear combination. These probability weighted moments can
be defined in terms of the cumulative distribution function F(x) as given
in (2.1-15) after [Gre79], where p,r, and s are positive
integers. x(F) denotes the quantile or inverse cumulative distribution
function of the random variable x.
The quantities may now be used to describe and characterize
probability distributions. If we express the probability weighted moments in
terms of the density function f(x) an alternative definition is given by
(2.1-16).
Note, that the moments 
are the noncentral conventional moments
(see 2.1-3). We shall instead use quantities 
where the
random variable x enters linearly, and in particular the moments 
given in (2.1-17), which we shall also refer to as PWMs.
Although probability weighted moments are useful to characterize a
distribution, they have no particularly meaning. It is
useful to define some functions of PWMs, which can be seen as descriptive
parameters of location, scale and shape of a probability function, the
L-moments. The linear combination between the L-moments
and the PWMs are given in (2.1-18) to
(2.1-21) for the first four moments.
We can describe a distribution by L-moments even when some of the conventional moments of the distribution do not exist. Therefore, only the mean value of the distribution must exist. The characterization of distributions by L-moments offers new possibilities such as the incorporation of up to now not considered density functions. These are the generalized gamma, generalized logistic, generalized pareto or the four-parameter kappa distribution function. It should be noted at this point that conventional density functions like the Gaussian or Pearson can not be defined over PWMs or L-moments, because the quantile function x(F) is not explicitly defined for these function.
To show the applicability of L-moments for ion implantation profiling, we introduce the four-parameter kappa distribution function to fit a dopant profile. All distribution functions F(x), f(x), and the quantile function x(F) are existing for the four-parameter kappa distribution and are given in (2.1-22),(2.1-23), and (2.1-24), respectively.
The four-parameter kappa distribution is a combination of the
generalized logistic, the generalized extreme-value and the generalized
Pareto distribution, where 
is a location parameter, 
a scaling
parameter and h,k shape parameters. The estimation of these characteristic
parameters based on L-moments requires a Newton-Raphson iteration
method, because no explicit solution of the probability weighted moments for
the kappa parameters is possible [Hos91].
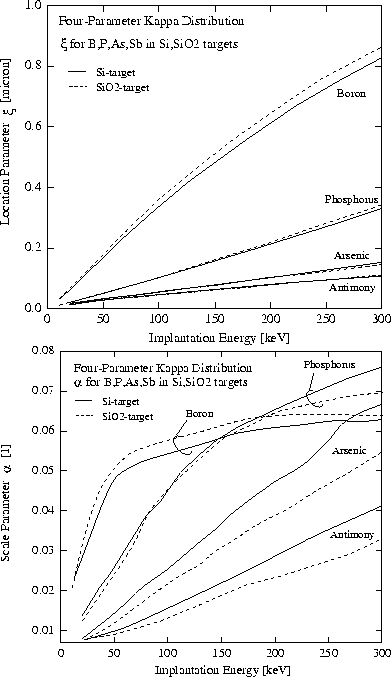
Figure 2.1-1: The location
parameter of the four-parameter kappa distribution functions for
different dopants, implantation targets and implantation energies.
Figure 2.1-2: The scale
parameter of the four-parameter kappa distribution functions for
different dopants, implantation targets and implantation energies.
In Figure 2.1-1 the location parameter of the four-parameter
kappa density function is shown for the most frequently used dopants and for
silicon and oxide implantation targets. The parameter acts similar to
the well-known projected range of conventional distributions. When the
implantation energy is increased the dopants penetrate deeper into the
substrate which leads to higher values for . The relationship between
and the implantation energy is about linear for phosphorus, arsenic
and antimony, only boron exhibits nonlinear behavior. The spread of the
kappa density function is controlled by the scale parameter
. Figure 2.1-2 shows the scale parameter with
respect to dopants, implantation targets and implantation energy. The higher
the scale parameter the broader the density function. By using
implantation energies above 100keV for boron implantations the scale
parameter tends to saturate. The other dopants show nearly linear dependence
to variation of the implantation energy.
Figure 2.1-3 shows the comparison of distributions obtained from central moments (Gauß, Pearson) and L-moments (Kappa). For non-symmetric profiles the four-parameter kappa distribution gives better results than the conventional distributions.
Figure 2.1-3: Comparison
of several analytical implantation profiles, based on central or
L-moments for a Boron implant at 40keV energy, 
dose, and 
tilt angle. The corresponding result of an amorphous
Monte Carlo simulation is also shown for reference purpose.
