


Next: 6.4 Large-Signal Measurements
Up: 6. Transistor Characterization
Previous: 6.2 Breakdown Voltages
For oscillator applications the low frequency 1/f noise is an extremely important quantity.
The upconversion of low frequency noise leads to widening of the frequency spectrum of the
oscillators' output signal. It is generally acknowledged [24] that the HEMT
shows inferior performance towards the HBT in terms of 1/f noise. However, if a HEMT
technology is inferior but available for a given chip set, it is useful to control variations of
the 1/f noise level to a certain extent. Similar to CMOS technologies where the 1/f
noise levels are part of the SIA Technology Roadmap [252] the 1/f levels are measured
with respect to several technology runs or variations. 1/f measurements were performed in a
system that was described in [30,154]. Fig. 6.17 shows a typical
measurement from an experiment performed:
Figure 6.17:
Comparison of the 1/f noise
between 0.5 Hz and 10 MHz for various transistor samples.
|
Nominally identical structures were processes with different test surface treatments
after recess etching. A relatively strong scattering is observed using different cleaning
procedures. Two conclusions can be drawn. First, the noise levels are subject to the
surface treatment, which was also reported in [79]. Second, for device modeling the
measurements supply a secondary piece of information: characteristic frequencies, respectively time
constants are extracted by the following procedure. To the first order, in [30,154] it
was found that a linear fit can be used to model the noise spectrum:
| |
|
 |
(6.1) |
which is suitable and indicated in Fig. 6.17.
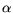 is the slope, which is close to unity. However, the
modeling can be improved. When measuring up to 10 MHz, as done in
Fig. 6.17, and after eliminating possible noise sources in
the measurement setup [30], specific trap time constants are
obtained by means of the following extraction procedure: The
spectral noise density
is the slope, which is close to unity. However, the
modeling can be improved. When measuring up to 10 MHz, as done in
Fig. 6.17, and after eliminating possible noise sources in
the measurement setup [30], specific trap time constants are
obtained by means of the following extraction procedure: The
spectral noise density
 is modeled as:
is modeled as:
The  are time constants introduced to model the impact of traps.
It was found by Bea in [30] that for the HEMTs under investigation adding two time
constants is sufficient representing two major traps in order to model the noise voltage in
(6.4). This allows to fit the trap contribution superimposed on the linear behavior, as
also described by [154]. Thus, characteristic time constants
are time constants introduced to model the impact of traps.
It was found by Bea in [30] that for the HEMTs under investigation adding two time
constants is sufficient representing two major traps in order to model the noise voltage in
(6.4). This allows to fit the trap contribution superimposed on the linear behavior, as
also described by [154]. Thus, characteristic time constants  are obtained
characterizing the dynamic trap behavior for the devices simulated. Dominant trap concentrations
are assumed at the SiN/barrier interface, as shown by Fig. 6.17, and in the bulk.
Table 6.1 gives typical frequencies obtained from the 1/f measurements, where the inverse
supplies time constants of the trap occupation.
are obtained
characterizing the dynamic trap behavior for the devices simulated. Dominant trap concentrations
are assumed at the SiN/barrier interface, as shown by Fig. 6.17, and in the bulk.
Table 6.1 gives typical frequencies obtained from the 1/f measurements, where the inverse
supplies time constants of the trap occupation.
Table 6.1:
Transient time constants obtained by 1/f measurements.
| Material |
f [MHz] |
Range [MHz] |
Al Ga Ga As/InGaAs HEMT As/InGaAs HEMT |
1 |
0.2-4 |
| InAlAs/InGaAs/InP HEMT |
0.4 |
0.02-2 |
|



Next: 6.4 Large-Signal Measurements
Up: 6. Transistor Characterization
Previous: 6.2 Breakdown Voltages
Quay
2001-12-21
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig81.eps}](img812.gif)