


Next: 3.1.4 Lattice Heat Flow
Up: 3.1 The Device Simulator
Previous: 3.1.2 Drift-Diffusion Current Relations
For the hydrodynamic (HD) transport model used in this work the
current densities are obtained for electrons as:
| |
|
 |
(3.6) |
and for holes:
| |
|
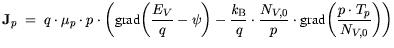 |
(3.7) |
Comparing to the DD approach the carrier temperature
 can deviate from the lattice temperature
can deviate from the lattice temperature
 .
The conservation of the average energy
.
The conservation of the average energy  is written:
is written:
| |
|
div grad grad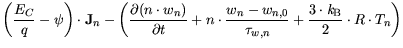 |
(3.8) |
| |
|
div grad grad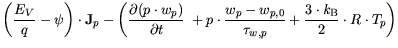 |
(3.9) |
The energy fluxes  are defined as:
are defined as:
| |
|
 grad grad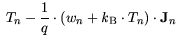 |
(3.10) |
| |
|
 grad grad |
(3.11) |
 and
and  denote the average carrier energies,
denote the average carrier energies,
 the equilibrium energies. The
the equilibrium energies. The  are
approximated as:
are
approximated as:
| |
|
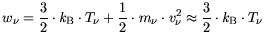 |
(3.12) |
The first term represents the carrier thermal energy
while the second denotes the carrier kinetic energy. In this work
the carrier kinetic energy is neglected against the thermal energy.
Some publications name the simplified transport model an energy transport model.
The impact of this simplification, which goes along with a limited number of moments considered for the solution of the Boltzmann equation,
and the results for device application from both numerical and accuracy aspects
are discussed in Section 3.6.
The carrier thermal conductivities
 are defined for electrons:
are defined for electrons:
| |
|
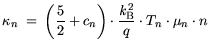 |
(3.13) |
and for holes:
| |
|
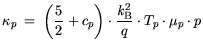 |
(3.14) |
(3.14) and (3.15) represent a generalized Wiedemann-Franz law. The heat capacities
 and
and  of the electron and hole gases are typically neglected.
of the electron and hole gases are typically neglected.



Next: 3.1.4 Lattice Heat Flow
Up: 3.1 The Device Simulator
Previous: 3.1.2 Drift-Diffusion Current Relations
Quay
2001-12-21