3.2.11.1 Impact Ionization for the Drift-Diffusion Transport Model

In the DD approximation the generation rates are usually calculated as:

$$G_i^{II} = \alpha_{i} \cdot \frac{\vert J_i\vert}{q}$$ (3.63)

with i = n,p and introduced into the continuity equation as:

$$R^{II} = -G_n -G_p$$ (3.64)

In a very straight forward model, e.g. for the use in diodes, the impact ionization rates can be modeled according to:

$$\alpha_{n}= \alpha_{n}^\infty \cdot \exp \bigg(-\bigg(\frac{E^{crit}_{n}\cdot\vert J_n\vert}{E\cdot J_n}\bigg)^{\beta_n}\bigg)$$ (3.65)

and

$$\alpha_{p} =  \alpha_{p}^\infty \cdot \exp \bigg(-\bigg(\frac{E^{crit}_{p}\cdot\vert J_p\vert}{E\cdot J_p}\bigg)^{\beta_p}\bigg)$$ (3.66)

This approach is very well known and widely used to compile the different sets of data suggested by the experiments. A number of sets, obtained from various measurement approaches, are summarized in Table 3.26.

Table 3.26: Impact Ionization parameters in bulk III-V binary semiconductors, diode: pn-diode measurements, MC: Monte Carlo simulation.

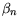Material	E	$\alpha_n$	E$^{crit}_n$	$\beta_n$	$\alpha_p$	E$^{crit}_p$	$\beta_p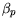$	Extraction	References
${\it T}_\mathrm{L}$, N$_D$	[V/cm]	[cm$^{-1}$]	[V/cm]		[cm$^{-1}$]	[V/cm]
GaAs		2.99e5	6.848e5	1.6	2.215e5	6.57e5	1.75	diode	[55]
		2.2e5	6.66e5	1.52	2.16e5	7.03e5	1.56	diode	[221]
AlAs		3.69e5	1.43e6	1.33	1.99e5	1.21e6	1.56	diode	[221]
InAs
77 K	5e4-3e5	1.09e5	9.8e4	1	-	-	-	MC	[91]
300 K	5e4-2.5e5	2.46e5	9.16e4	1	-	-	-	MC	[91]
300 K	5e3-1e5	1.25e5	3.6e4	1	-	-	-	MC	[52]
InP
1.2e15	2.4-3.6e5	1.12e7	3.11e6	1	4.79e6	2.55e6	1	diode	[67]
3.0e16	3.6-5.6e5	2.93e6	2.64e6	1	1.62e6	2.11e6	1	diode	[67]
1.2e17	5.3-7.7e5	2.32e5	8.46e5	2	2.48e5	7.89e5	2	diode	[67]
GaN	2-4.05e6	1.4e7	1.48e7	1.40	2.95e5	5.17e6	2	MC	[200]
	3-3.75e6	8.9e6	1.05e7	2	-	-	-	MC	[149]

In order to sort and qualify these, the extraction procedure is additionally named. The direct comparison of the model parameters is rendered complicated, since the parameters $\beta$ are not always used for fitting and set to 1. However, principal tendencies can be observed. A relatively stable database is available for GaAs. 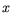The value for AlAs is found from fitting of the material composition of Al$_x$Ga$_{1-x}$As for $x$= 0..0.6. For InAs, the soft onset of impact ionization cannot be modeled very well with equations (3.68) and (3.69). Thus, the fit is only valid for the range of the electric field indicated in Table 3.26. However, some observations can be made which are the low breakdown field and the positive temperature coefficient of the InAs parameters. For InP the doping dependence can be evaluated, which reduces impact ionization for higher impurity concentrations. For GaN only preliminary data are available for comparably higher fields than for the GaAs based materials. The high critical fields extracted show the breakdown hardness of this materials system due to the large band gap.

Parameters for different material compositions of ternary compounds from the above basic materials are listed in Table 3.27. For most of the compositions of Al$_{x}$Ga$_{1-x}$As and for In$_{0.52}$Al$_{0.48}$As measurements are available. The data from [297] and [309] has been used for HEMT simulation in [281].

Table 3.27: Impact ionization parameters in bulk III-V ternary semiconductors.

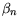Material	Mat. Comp.	$\alpha_n$	E$^{crit}_n$	$\beta_n$	$\alpha_p$	E$^{crit}_p$	$\beta_p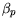$	Extraction	References
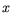	$x$	[cm$^{-1}$]	[V/cm]		[cm$^{-1}$]	[V/cm]
AlGaAs	0.1	1.81e5	6.31e5	2	3.05e5	7.22e5	1.9	diode	[232]
	0.15	2.17e5	7.74e5	1.533	2.51e5	8.60e5	1.516	diode	[221]
	0.2	1.09e6	1.37e6	1.3	6.45e5	1.11e6	1.5	diode	[232]
	0.3	2.21e5	7.64e5	2.0	2.79e5	8.47e5	1.9	diode	[232]
	0.3	2.69e5	9.54e5	1.476	3.20e5	1.06e6	1.43	diode	[221]
	0.4	1.74e7	3.39e6	1.0	3.06e6	2.07e6	1.2	diode	[232]
	0.6	2.95e7	1.16e8	1.44	3.11e5	1.215e6	1.433	diode	[221]
InGaAs	0.53	5.9e5	1.33e6	1	1e6	1.63e6	1	diode	[205]
	0.53	6.9e4	9e5	1	1.15e6	1.7e6	1	diode	[297]
InAlAs	0.52	7.36e4	5.62e5	2	1.57e4	4.88e5	2	diode	[59]
	0.52	8.6e6	3.5e6	1	2.3e7	4.5e6	1	diode	[309]
InGaP	0.48	4.57e5	1.413e6	1.73	4.73e5	1.425e6	1.65	diode	[102]
	0.5	3.85e6	3.71e6	1	1.71e6	3.195e6	1	diode	[97]

For those data sets which were presented consistently for various material compositions, the following formulae are applied to model the material dependence of the impact ionization parameters.The extracted parameters for Al$_{x}$Ga$_{1-x}$As are given in Table 3.28 and shown in Fig. 3.16, where a systematic material dependence can be observed.

$$\centering\alpha_{i,AB} = x \cdot \alpha_A + (1-x) \cdot \alpha_B + x \cdot (1-x) \cdot \alpha_{AB}$$ (3.67)

$$\beta_{i,AB} = x \cdot \beta_A + (1-x) \cdot \beta_B + x \cdot (1-x) \cdot \beta_{AB}$$ (3.68)

$$E_{i,AB} = x \cdot E_{i, A} + (1-x)\cdot E_{i, B} + x \cdot (1-x) \cdot E_{i, AB}$$ (3.69)

Table 3.28: Impact ionization parameters for the model in bulk III-V ternary semiconductors [221].

Material	Valid for 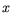$x$	$\alpha_{n,AB}$	$\beta_{n,AB}$	E$_{n,AB}$	$\alpha_{p,AB}$	$\beta_{p,AB}$	E$_{p,AB}$	Refs.
		[cm$^{-1}$]		[V/cm]	[cm$^{-1}$]		[V/cm]
Al$_{x}$Ga$_{1-x}$As	0-0.6	-5.1e4	1.44	1.75e5	4.45e4	-0.54	8.66e5	[221]

Figure 3.16: Impact ionization parameters as a function of material composition for Al$_x$Ga$_{1-x}$As [221].

Figure 3.17: Impact ionization rates as a function of material composition for In$_x$Al$_{1-x}$As [60,91,221,309].

Fig. 3.17 shows the data available for the typical barrier material In$_{x}$Al$_{1-x}$As. The experimental situation for In$_{0.52}$Al$_{0.48}$As is indicated. The plot is useful for the modeling of different material compositions in metamorphic HEMTs. For InAs MC data from [91] are taken. For AlAs data from the extraction in Table 3.28 are assumed.

For HEMT simulation it is extremely desirable to model the temperature dependence of the impact ionization rates for ${\it T}_\mathrm{L}$$>$ 300 K in order to understand the interaction between electrically and thermally induced device and performance degeneration. Unfortunately, very little data are available to extract the dependence for the layer materials In$_{0.25}$Ga$_{0.75}$As and In$_{0.48}$Al$_{0.52}$As. For In$_{0.53}$Ga$_{0.47}$As in [193] a positive temperature coefficient was reported resulting in increasing impact ionization with rising ${\it T}_\mathrm{L}$. Fig. 3.18 shows the dependence in GaAs for electron and holes, where impact ionization decreases as function of ${\it T}_\mathrm{L}$. In Fig. 3.19 the extracted model parameters from a consistent set of measurement data from [285] for InP are given versus temperature. The data for $\alpha_{i}$ and $E_{crit,i}$, also presented in Table 3.29, show a systematic increase of the critical field versus ${\it T}_\mathrm{L}$. 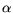$\alpha$ first rises and drops above a certain ${\it T}_\mathrm{L}$. However, the overall temperature coefficient of the impact ionization rates is negative for the temperatures observed. Recently, measurement data for Al$_{x}$Ga$_{1-x}$As were published [326], very unfortunately, the paper contains several inconsistencies in data and comparisons applied.

Figure 3.18: Impact ionization parameters versus temperature for a given field in GaAs [60].

Figure 3.19: Impact ionization parameters versus temperature in InP [285].

Table 3.29 gives data sets compiled in the form of (3.68) and (3.69).

Table 3.29: Measured impact ionization parameters for InP as a function of lattice temperature.

Material	${\it T}_\mathrm{L}$	$\alpha_n$	E$^{crit}_n$	$\beta_{n}$	$\alpha_p$	E$^{crit}_p$	$\beta_{p}$
	[K]	[cm$^{-1}$]	[V/cm]		[cm$^{-1}$]	[V/cm]
InP	298	9.2e6	3.44e6	1	4.3e6	2.72e6	1
	373	1.22e7	3.73e6	1	1.06e7	3.36e6	1
	398	1.026e7	3.78e6	1	1.39e7	3.63e6	1
	448	1.04e7	3.89e6	1	1.06e7	3.56e6	1

To obtain a more systematic view of the temperature dependence also for other materials the following approach is used: In [64] Chau and Pavlidis compiled available sets of data, as given in the previous section, into the Okuto-Crowell model [202]. The Baraff approach [26] is used there with its lattice temperature dependence to establish a base for an estimate of impact ionization data at unknown temperatures and material compositions. A similar approach is taken here for such materials which have a similar temperature dependence as GaAs, i.e., Al$_{x}$Ga$_{1-x}$As, and InP. Contrary to [64] this work does not include In$_{x}$Ga$_{1-x}$As for $x_{crit}$$\geq$ 0.53, where the temperature coefficient is positive, as was shown in [75,193]. An even lower bound for this critical In content $x_{crit}$, where the temperature coefficient of InGaAs changes its sign, is discussed in Chapter 7.

The Okuto-Crowell impact ionization model basically is a modification of (3.68) and (3.69), where three parameters enter the formula:

$$\alpha_{n,p} = \bigg(\frac{qF}{E_i}\bigg) \bigg(0.217\bigg(\frac{E_i}{E_r}\bigg)^{1.14}- \bigg\{\bigg[ 0.21... ...\bigg)^{1.14}\bigg]^2 +\bigg(\frac{E_i}{qF\lambda}\bigg)^2 \bigg\}^{0.5} \bigg)$$ (3.70)

$E_i$ is a threshold energy, $E_r$ is the average energy loss per scattering, and $\lambda$ the mean free path for the optical phonon scattering. The temperature dependence of (3.73) is introduced in (3.74) and (3.75).

$$E_{r} = \displaystyle E_{0,r} \tanh \bigg(\frac{E_{r0}}{2 {\it k}_{\mathrm{B}}\cdot {\it T}_\mathrm{L}} \bigg)$$ (3.71)

$$\lambda = \displaystyle \lambda_{0} \tanh \bigg(\frac{E_{r0}}{2 {\it k}_{\mathrm{B}}\cdot {\it T}_\mathrm{L}} \bigg)$$ (3.72)

Model parameters are compiled in Table 3.30. The data given include the modifications as stated by Chau and Pavlidis in [64]. Thus, for the materials used in this work a systematic scheme is found to fill the gaps of the data base as function of temperature. This presents a consistent approach to the lattice temperature dependence to support the modeling in the hydrodynamic model in the next section.

Table 3.30: Impact ionization rates according to the modeling approach.

Material	$\nu$	Composition	$E_{i,n}$	$E_{i,p}$	$E_{r,0}$	$\lambda_0$	$E_r$	$\lambda$
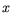		$x$	[eV]		[meV]	Å	[meV]	Å
GaAs	n,p	-	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$+0.52	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$+0.7	43	60.65	29.3	50
InP	n,p	-	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$+0.16	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$-0.21	52.15	56.6	39.9	45.2
Al$_x$Ga$_{1-x}$As	n,p	0.1	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.18	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.31	45.12	53	31.7	40.9
	n,p	0.2	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.51	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.64	47.1	54.17	34	42.3
	n,p	0.3	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.68	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.86	48.06	55.6	35.1	44
	n,p	0.4	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.69	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$ +0.94	50.45	55.95	37.9	44.4
In$_{x}$Al$_{1-x}$As	n,p	0.52	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$+0.71	${\it E}_\mathrm{g}({\it T}_\mathrm{L})$+1.31	45.37	45.45	32	32