B.2.2 Second-Order Loop

Figure B.4: Second-order sigma-delta converter (noise model)

Similar expressions as above can be derived for a second-order converter shown in Fig. B.2, based on the model shown in Fig. B.4. In this case a second source of error (e₁) originating from the non-linearities of the first integrator. The unfiltered output Y(s) is then

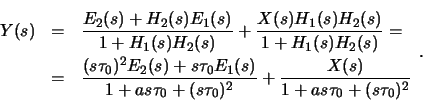$$\renewcommand{\arraystretch}{2.0} { \begin{array}{rcl} Y(... ...playstyle\frac{X(s)}{1+a s\tau_0+(s\tau_0)^2}} \end{array}}.$$ (B.8)

Ideally, if e₁ = 0, the noise power spectral density would be proportional to $(s\tau_0)^2$, which should result in a much better SNR if the converter is properly designed.