D.3 Scalability of adiabatic CMOS

Returning to Fig. D.2 with real MOSFETs as switches it becomes clear that the finitely large subthreshold leakage not only contributes to the switching energy but also changes the asymptotic behavior. Assuming, for simplicity,

$$\begin{eqnarray*}\ensuremath{{\mathit{ld}}}\xspace &=& \ensuremath{{\mathit{ar}}... ...ath{V_{\mathit{T}}}\xspace /\ensuremath{U_{\mathit{T}}}\xspace } \end{eqnarray*}$$

we can write an equation for the switching energy in an adiabatic CMOS circuit:

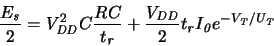$$\frac{\ensuremath{E_{\mathit{s}}}\xspace }{2} = \ensuremath... ...h{V_{\mathit{T}}}\xspace /\ensuremath{U_{\mathit{T}}}\xspace }$$ (D.2)

This means that for a fixed threshold voltage the switching energy has a finite minimum value. Further analysis shows that for minimum , where $\ensuremath{V_{\mathit{T}}}\xspace = \ensuremath{V_{\mathit{DD}}}\xspace /2$, the switching energy and rise time are related to the supply voltage as

$$\ensuremath{E_{\mathit{s}}}\xspace = 4 C \sqrt{\frac{\ensuremath{I_{\mathit{0}}}\xspace }{\beta}} \ens... ...^{-\ensuremath{V_{\mathit{DD}}}\xspace /{4\ensuremath{U_{\mathit{T}}}\xspace }}$$ (D.3)

$$\ensuremath{t_{\mathit{r}}}\xspace = 2 C \sqrt{\frac{1}{\ensuremath{I_{\mathit{0}}}\xspace \beta}} e^{\ensuremath{V_{\mathit{DD}}}\xspace /{2\ensuremath{U_{\mathit{T}}}\xspace }},$$ (D.4)

which means that the scalability of adiabatic CMOS is limited not only by the overhead required to compensate for the performance loss but also by the maximum affordable supply voltage.