3.1.2 Interconnect Delay

Interconnections contribute to the delay time two-fold: by capacitive loading and by distributed-RC delay. The interconnect capacitance $\ensuremath{c_{\mathit{M}}}\xspace \ensuremath{L_{\mathit{M}}}\xspace$ adds to the capacitive load of the driving stages. This effect dominates for short interconnections. Interconnect capacitance can be determined accurately with two and three-dimensional device simulation [6,60]. For some purposes there are also analytical models [5,36], which can also be calibrated to simulated or measured data. The interconnect RC delay

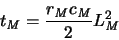$$\ensuremath{t_{\mathit{M}}}\xspace = \frac{\ensuremath{r_{\... ...\mathit{M}}}\xspace }{2} \ensuremath{L_{\mathit{M}}}\xspace ^2$$ (3.4)

dominates for long interconnections. Clearly, long interconnections will be avoided by inserting repeaters to eliminate the square-law length dependence and to regenerate the signal. However, as the feature size is scaled down $\ensuremath{r_{\mathit{M}}}\xspace = \ensuremath{\rho _{\mathit{M}}}\xspace \ensuremath{W_{\mathit{M}}}\xspace \ensuremath{H_{\mathit{M}}}\xspace$ increases by $\ensuremath{\kappa }\xspace ^2$ and remains constant so that the interconnect RC-delay does not scale with feature size. This is a serious problem in deep-sub-micron technologies, where interconnect delay starts to dominate [7,8,35].