3.1.3 Device Delay

A single transistor cannot be characterized like a complete digital circuit. However, a transistor delay determined from key device data is strongly related to gate delay and system speed. The simplest expression for this is the so-called CV/I delay metric, where a delay time is computed as

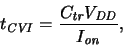$$\ensuremath{t_{\mathit{CVI}}}\xspace = \frac{\ensuremath{C_... ...\mathit{DD}}}\xspace }{\ensuremath{I_{\mathit{on}}}\xspace } ,$$ (3.5)

where mostly $\ensuremath{C_{\mathit{tr}}}\xspace = \ensuremath{\epsilon _{\mathit{i}}}\xspac... ...nsuremath{W}\xspace \ensuremath{L}\xspace /\ensuremath{t_{\mathit{ox}}}\xspace$ (neglecting diffusion and miller capacitance). (3.5) renders a delay time which is in the order of the actual circuit delay and shows a similar dependence on technology and operating parameters. The CV/I metric is therefore very handy for simple trend analyses. Apart from using analytical equations for and these quantities can be also measured or simulated directly. An accurate alternative method for determining $\ensuremath{C_{\mathit{tr}}}\xspace = \ensuremath{Q_{\mathit{sw}}}\xspace /\ensuremath{V_{\mathit{DD}}}\xspace$ is given in Section 3.3.5. Another way to account for device delay is to embed transistors in a switch-level RC model, i.e., to compute an effective resistance so that

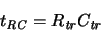$$\ensuremath{t_{\mathit{RC}}}\xspace = \ensuremath{R_{\mathit{tr}}}\xspace \ensuremath{C_{\mathit{tr}}}\xspace %$$ (3.6)

For the CV/I metric the resistance would be $\ensuremath{R_{\mathit{tr}}}\xspace = \ensuremath{V_{\mathit{DD}}}\xspace /\ensuremath{I_{\mathit{on}}}\xspace$.