2.4.1 Transmission Probability

  A wave packet with a probability amplitude B₁ hits a potential barrier. Part of the wave will be reflected and the rest will be transmitted through the barrier. The probability amplitude of the transmitted part is denoted by B₃. The transmission probability |T|² is defined as the square of the ratio between transmitted and incoming probability amplitudes
$$\begin{gather}\vert T\vert^2 = \frac{\vert B_3\vert^2}{\vert B_1\vert^2}. \end{gather}$$

The transmission probability can be derived from Schrödinger's equation
$$\begin{gather}H\psi = E\psi. \end{gather}$$
For a rectangular potential barrier with width d and height E₀ it is (see Appendix C.3 for a derivation)
$$\begin{gather}\vert T\vert^2 = \frac{\vert B_3\vert^2}{\vert B_1\vert^2} = \lef... ...*E} \qquad\text{and}\qquad k_2 = \frac{1}{\hbar}\sqrt{2m^*(E_0-E)} \end{gather}$$
For a typical  strength parameter $d\sqrt{\smash[b]{2m^*E_0}}/\hbar$ of 30 the transmission probability is shown in Fig. 2.4. The strength parameter allows a classification of tunnel barriers according to their  opaqueness.

  

Figure 2.4: Transmission probability for a barrier with a strength parameter of 30, 10, 5, and 1.

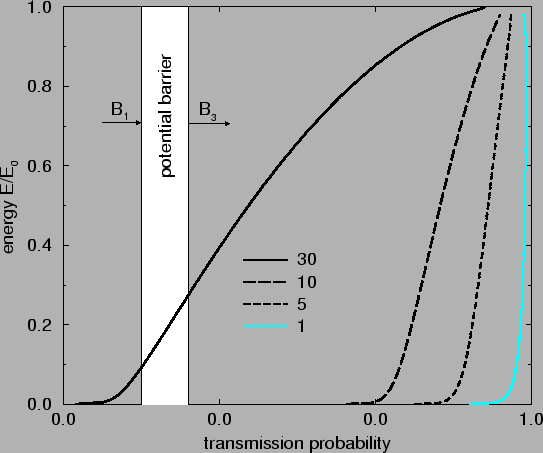A strength parameter of 1 is typical of the barriers present in most ohmic contacts to semiconductors, a value of 5 is typical for the ionization of an atom by an electric field and a value of 30 is characteristic for the $\alpha$-decay from a radioactive nucleus [47].