3.4.2 Fluxes




Next: Diffusion Fluxes
Up: 3.4 Discretization of the
Previous: 3.4.1 Divided Differences
Our expressions derived for the transformed differential operators are the
result of a box integration over subdomains  . These subdomains
partition the interior of the simulation domain without overlap or
exclusion. It is quite obvious to use subdomains
. These subdomains
partition the interior of the simulation domain without overlap or
exclusion. It is quite obvious to use subdomains  (3.4-7)
that split the domain at the mid interval lines of the grid
(Figure 3.4-3), which are identical to the Voronoi cells
(cf. Figure 3.3-1).
(3.4-7)
that split the domain at the mid interval lines of the grid
(Figure 3.4-3), which are identical to the Voronoi cells
(cf. Figure 3.3-1).


We use the common notation for function values at mid interval points
(3.4-8), (3.4-9) and the grid spacing in the
computational domain (3.4-10).



In the following we repeatedly require discrete approximations for partial
derivatives of a function  . If
. If  is sufficiently smooth (here three
times differentiable), we may use the difference expression
(3.4-11) for the partial derivatives. The local truncation error
is sufficiently smooth (here three
times differentiable), we may use the difference expression
(3.4-11) for the partial derivatives. The local truncation error
 is the residual which occurs when inserting the solution of the
continuous problem into the discrete scheme. The local truncation error in
our approximation (3.4-11) is of first order in the grid spacing
weighted with the second partial derivatives (3.4-12).
Therefore, we call the approximation (3.4-11) first order
accurate.
is the residual which occurs when inserting the solution of the
continuous problem into the discrete scheme. The local truncation error in
our approximation (3.4-11) is of first order in the grid spacing
weighted with the second partial derivatives (3.4-12).
Therefore, we call the approximation (3.4-11) first order
accurate.


The most crucial and computationally expensive task is to find an
appropriate discrete representation for the flux components. To avoid
unnecessary complications we look closely at just one term of the sum in
(3.1-2), at the partial flux  of quantity
of quantity  which
is related to (or driven by) quantity
which
is related to (or driven by) quantity  . The transformation of the
equations from physical space
. The transformation of the
equations from physical space  to computational space
to computational space  is linear and,
therefore, we can merely consider the term
is linear and,
therefore, we can merely consider the term

and then discretize its transformed counterpart and accumulate the
discretized fluxes, without loss of generality. The term  is not
explicitly indicated in the following derivations. It is treated as an
independent additional contribution to the flux
is not
explicitly indicated in the following derivations. It is treated as an
independent additional contribution to the flux  .
.
The transformed flux is given by (3.4-14) and
(3.4-15), which is obtained by applying (3.3-55)
to (3.4-13).

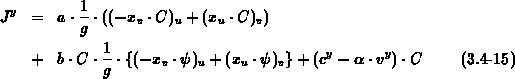
For the transformed expression of the divergence (3.4-16), we
need both flux components  and
and  at all mid interval points
at all mid interval points
 and
and  . These points are marked by
. These points are marked by  in
Figure 3.4-3.
in
Figure 3.4-3.

For the discretization of these flux components  and
and  at a mid
interval point
at a mid
interval point  we use the local vertical six point stencil shown
in Figure 3.4-4. We denote values at the fictive center point
(
we use the local vertical six point stencil shown
in Figure 3.4-4. We denote values at the fictive center point
( ) with an index
) with an index  and the neighbor points (
and the neighbor points ( ) which are
actual grid points with indices 1 to 6. For the mid interval point
) which are
actual grid points with indices 1 to 6. For the mid interval point
 we use the analogous horizontal six point stencil.
we use the analogous horizontal six point stencil.

For numerical reasons we distinguish between the cases where we have
- -
- only a diffusive flux,
- -
- only a convective flux,
- -
- diffusive and convective flux.




Next: Diffusion Fluxes
Up: 3.4 Discretization of the
Previous: 3.4.1 Divided Differences
Martin Stiftinger
Wed Oct 19 13:03:34 MET 1994
 . These subdomains
partition the interior of the simulation domain without overlap or
exclusion. It is quite obvious to use subdomains
. These subdomains
partition the interior of the simulation domain without overlap or
exclusion. It is quite obvious to use subdomains  (3.4-7)
that split the domain at the mid interval lines of the grid
(Figure 3.4-3), which are identical to the Voronoi cells
(cf. Figure 3.3-1).
(3.4-7)
that split the domain at the mid interval lines of the grid
(Figure 3.4-3), which are identical to the Voronoi cells
(cf. Figure 3.3-1).









 . If
. If  is the residual which occurs when inserting the solution of the
continuous problem into the discrete scheme. The local truncation error in
our approximation (
is the residual which occurs when inserting the solution of the
continuous problem into the discrete scheme. The local truncation error in
our approximation (

 of quantity
of quantity  which
is related to (or driven by) quantity
which
is related to (or driven by) quantity  . The transformation of the
equations from physical space
. The transformation of the
equations from physical space  to computational space
to computational space  is linear and,
therefore, we can merely consider the term
is linear and,
therefore, we can merely consider the term

 is not
explicitly indicated in the following derivations. It is treated as an
independent additional contribution to the flux
is not
explicitly indicated in the following derivations. It is treated as an
independent additional contribution to the flux  .
.

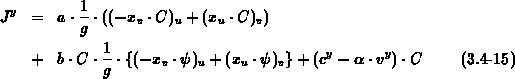
 and
and  at all mid interval points
at all mid interval points
 and
and  . These points are marked by
. These points are marked by  in
Figure
in
Figure 
 we use the local vertical six point stencil shown
in Figure
we use the local vertical six point stencil shown
in Figure  and the neighbor points (
and the neighbor points ( ) which are
actual grid points with indices 1 to 6. For the mid interval point
) which are
actual grid points with indices 1 to 6. For the mid interval point
 we use the analogous horizontal six point stencil.
we use the analogous horizontal six point stencil.
