next up previous contents
Next: 4.1.3 High Values of Up: 4.1 Unprimed Subbands Previous: 4.1.1 Scaled Energy Dispersion

4.1.2 Small Strain Values

The valley splitting was shown to be linear in strain for small shear strain values and to depend strongly on the film thickness [181]. To support these findings we reformulated (4.14) for the sum and the difference of $ X_{1}$ and $ X_{2}$. First we introduce the transformation rules for $ y_{n}$ and $ \bar{y}_{n}$ as,

$\displaystyle y_{n} = \frac{X_{1}-X_{2}}{2} \quad\mathrm{and}\quad \bar{y}_{n} = \frac{X_{1}+X_{2}}{2}\quad\:$ (4.17)

or

$\displaystyle (y_{n}+\bar{y}_{n})^{2}= X_{1}^{2} \quad\mathrm{and}\quad (y_{n}-\bar{y}_{n})^{2}= X_{2}^{2}\enspace.$ (4.18)

We only show the derivation for (4.14a), due to the similarity with (4.14b). Using the above given transformation and rewriting (4.14a) to separate $ y_{n}$ and $ \bar{y}_{n}$ leads to the following expression.

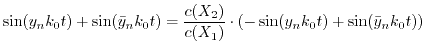$\displaystyle \sin(y_{n} k_{0} t) + \sin(\bar{y}_{n} k_{0} t)= \frac{c(X_{2})}{c(X_{1})} \cdot \left(-\sin(y_{n} k_{0} t) + \sin(\bar{y}_{n} k_{0} t)\right)$ (4.19)

Further simplification steps result in:

$\displaystyle \sin(y_{n} k_{0} t) = \frac{c(X_{2})-c(X_{1})}{c(X_{2})+c(X_{1})}\, \sin(\bar{y}_{n} k_{0} t)$ (4.20)

Now we re-express $ \bar{y}_{n}$ as function of $ y_{n}$ (Appendix B.) resulting in

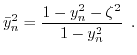$\displaystyle \bar{y}_{n}^{2} = \frac{1-y_{n}^{2}-\zeta^{2}}{1-y_{n}^{2}}\enspace.$ (4.21)

The derivation of the fraction containing $ c(X_{1})$ and $ c(X_{2})$ can be found in Appendix B..

$\displaystyle \sin(y_{n} k_{0} t)=\pm \frac{\zeta\, y_{n} \sin\left(\sqrt{\frac... ...^{2}}{1-y_{n}^{2}}} k_{0}t\right)}{\sqrt{(1-y_{n}^{2})(1-\zeta^{2}-y_{n}^{2})}}$ (4.22)

For zero stress the ratio on the right hand side of (4.22) is equal to zero, and the standard quantization condition $ q_{n}=\pi n/k_{0}t$ is recovered. Due to the plus/minus sign in the right-hand side of (4.22), the equation splits into two non-equivalent branches for $ \zeta\neq0$ and non-parabolic bands. (4.22) is nonlinear and can be solved only numerically. However, for small $ \zeta $ the solution can be thought in the form $ y_{n}=q_{n}\pm\zeta$, where $ \zeta $ is small. Substituting $ y_{n}=q_{n}$ into the right-hand side of (4.22) and solving the equation with respect to $ \zeta $, we obtain for the valley splitting:

$\displaystyle \Delta E_{n}=4 \left(\frac{\pi n}{k_{0} t}\right)^{2} \frac{\Xi_{u'} \varepsilon_{xy}}{k_{0} t}\, \frac{\sin(k_{0} t)}{\vert 1-q_{n}^{2}\vert}$ (4.23)

In accordance with earlier publications [182,183,184,185], the valley splitting is inversely proportional to the third power of $ k_{0}$ and the third power of the film thickness $ t$. The value of the valley splitting oscillates with film thickness, in accordance with [183,184,185]. In contrast to previous works, the subband splitting is proportional to the gap $ \delta$ at the X-point, and not at the $ \Gamma$-point. Since the parameter $ \zeta $, which determines non-parabolicity, depends strongly on shear strain, the application of uniaxial [110] stress to [001] ultra-thin Si film generates a valley splitting proportional to strain.

next up previous contents
Next: 4.1.3 High Values of Up: 4.1 Unprimed Subbands Previous: 4.1.1 Scaled Energy Dispersion
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors