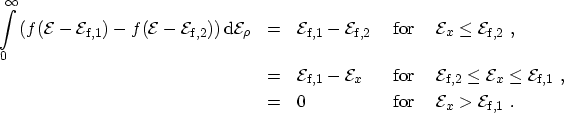A. The FOWLER-NORDHEIM Formula

The TSU-ESAKI expression (3.12) for the tunnel current density reads

$$J=\frac{4 \pi \ensuremath {\mathrm{q}}\ensuremath{m_\mathrm{eff}}... ...}) -f_2({\mathcal{E}})\right) \, \ensuremath {\mathrm{d}}{\mathcal{E}}_\rho \ ,$$ (A.1)

where the total energy is split into a longitudinal and a transversal energy

$${\mathcal{E}}={\mathcal{E}}_{x}+{\mathcal{E}}_{\rho}\ .$$ (A.2)

The goal is to find a simple approximation of (A.1) which avoids numerical integration. As a first approximation, $T \to 0$ is assumed [96]. This allows to replace the FERMI function $f(x)$ by the step function

$$\begin{array}{l} f_1({\mathcal{E}}) = f({\mathcal{E}}-\ensure... ...{{\mathcal{E}}_\mathrm{f,2}}\end{array} \right. \ . \end{array}$$ (A.3)

Without loss of generality it can be assumed that $\ensuremath{{\mathcal{E}}_\mathrm{f,1}} > \ensuremath{{\mathcal{E}}_\mathrm{f,2}}$ (see Fig. A.1). The innermost integral can then be evaluated analytically for three distinct regions

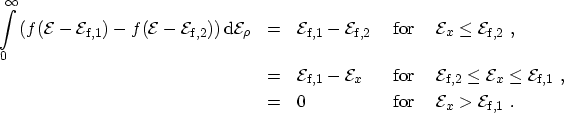$$\begin{array}{rclcl} \displaystyle \int_0^\infty \left( f({\m... ...{E}}_x > \ensuremath{{\mathcal{E}}_\mathrm{f,1}}\ . \end{array}$$ (A.4)

This leads to the following expression for the current density:

$$J=\frac{4\pi \ensuremath {\mathrm{q}}\ensuremath{m_\mathrm{eff}}}... ...m{f,1}}- {\mathcal{E}}_x) \,\ensuremath {\mathrm{d}}{\mathcal{E}}_x \right) \ .$$ (A.5)

The left integral represents tunneling current from electron states that are low in energy and face a high energy barrier. Hence, as a second approximation, the left integral is neglected. Still it is necessary to insert an expression for the transmission coefficient in the right integral. For a single-layer dielectric, two shapes are possible: triangular and trapezoidal. First, the formula will be derived assuming a triangular shape.

Figure A.1: Energy barrier in the FOWLER-NORDHEIM tunneling (left) and direct tunneling (right) regime.

Subsections

• A.1 Original FOWLER-NORDHEIM Formula
• A.2 Correction for Direct Tunneling

A. Gehring: Simulation of Tunneling in Semiconductor Devices